Question
Question: Q fmd value of K for which $6x^2+11xy-10y^2+x+31y+k=0$ rep. Pair of STL....
Q fmd value of K for which 6x2+11xy−10y2+x+31y+k=0 rep. Pair of STL.
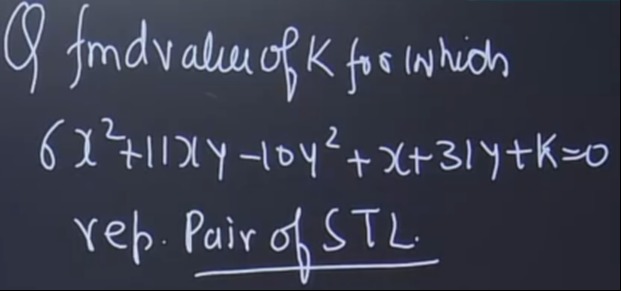
-15
Solution
The given equation is 6x2+11xy−10y2+x+31y+k=0. This is a general second-degree equation of the form ax2+2hxy+by2+2gx+2fy+c=0. Comparing the given equation with the general form, we identify the coefficients: a=6
2h=11⟹h=211
b=−10
2g=1⟹g=21
2f=31⟹f=231
c=k
A general second-degree equation represents a pair of straight lines if and only if the determinant of the matrix of coefficients is zero:
ahghbfgfc=0
Expanding the determinant, the condition is abc+2fgh−af2−bg2−ch2=0.
Substitute the values of the coefficients into this condition: a=6,b=−10,c=k,h=211,g=21,f=231
abc=(6)(−10)(k)=−60k
2fgh=2(231)(21)(211)=431×11=4341
af2=6(231)2=6×4961=23×961=22883
bg2=(−10)(21)2=−10×41=−410=−25
ch2=k(211)2=k×4121=4121k
Substitute these terms into the determinant condition: −60k+4341−22883−(−25)−4121k=0
To eliminate fractions, multiply the entire equation by 4: 4(−60k)+4(4341)−4(22883)−4(−25)−4(4121k)=0
−240k+341−2(2883)−2(−5)−121k=0
−240k+341−5766+10−121k=0
Group the terms with k and the constant terms: (−240k−121k)+(341+10−5766)=0
−361k+(351−5766)=0
−361k−5415=0
−361k=5415
k=−3615415
To simplify the fraction, we can test for common factors. We know 361=192. Divide 5415 by 19: 5415÷19=285. Divide 285 by 19: 285÷19=15. So, 5415=19×285=19×19×15=361×15.
Therefore, k=−361361×15=−15.
The value of k for which the given equation represents a pair of straight lines is −15.
