Question

find time taken by liq to Decrease level of liq. from H to h

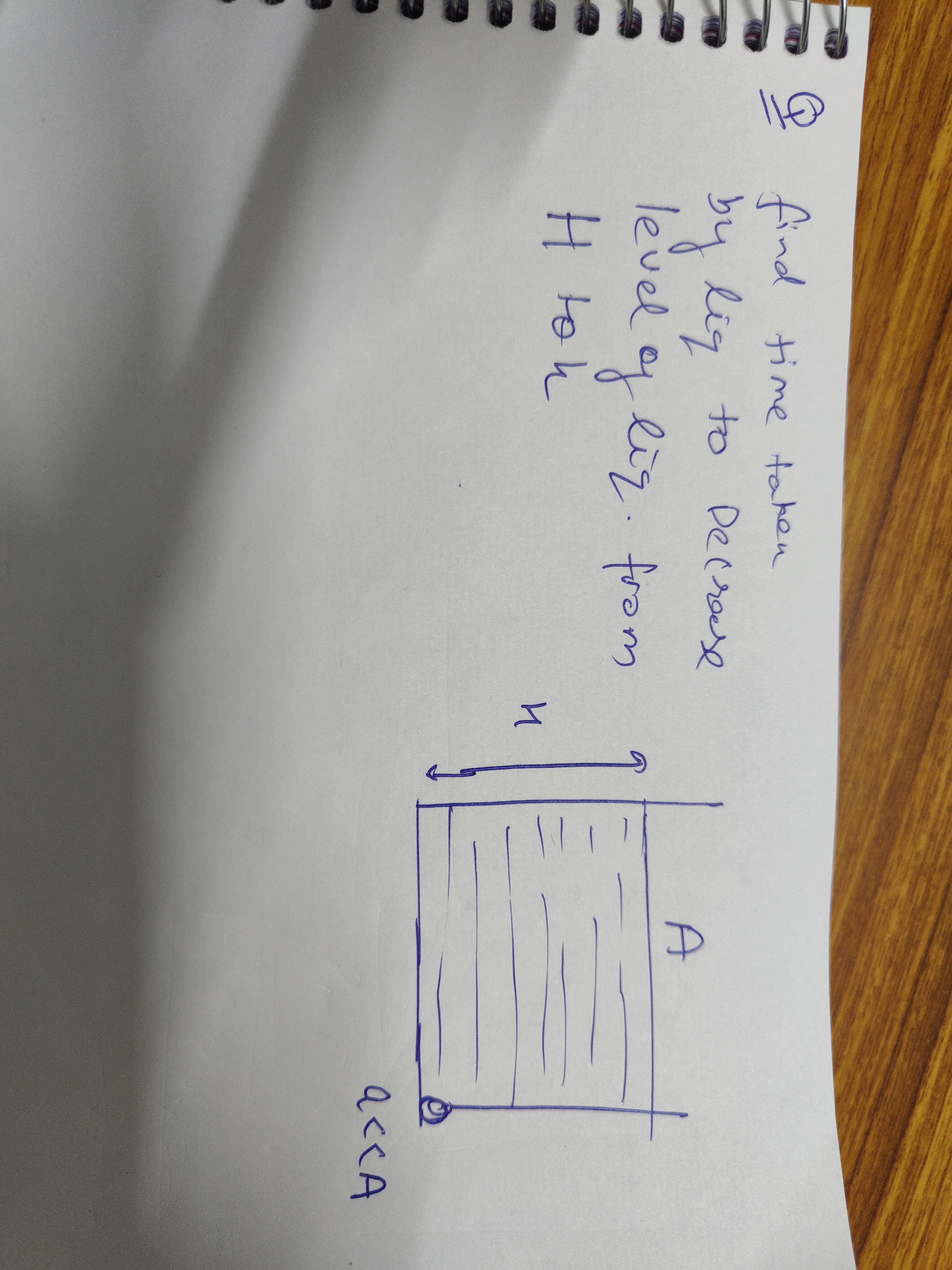
• A. A

Answer 1

The time taken for the liquid level to decrease from height $H$ to height $h$ is given by $T = \frac{A}{a}\sqrt{\frac{2}{g}}(\sqrt{H} - \sqrt{h})$.

Answer 2

The velocity of efflux from the hole at height $y$ is $v = \sqrt{2gy}$ (Torricelli's Law).

The rate of volume flow out is $Q = av = a\sqrt{2gy}$.

The rate of change of volume in the tank is $A \frac{dy}{dt}$. Since the volume is decreasing, $A \frac{dy}{dt} = -Q$.

So, $A \frac{dy}{dt} = -a\sqrt{2gy}$.

Separating variables: $\frac{dy}{\sqrt{y}} = -\frac{a}{A}\sqrt{2g} \, dt$.

Integrating from $t=0$ (height $H$) to $t=T$ (height $h$): $\int_{H}^{h} y^{-1/2} \, dy = -\frac{a}{A}\sqrt{2g} \int_{0}^{T} \, dt$ $[2\sqrt{y}]_{H}^{h} = -\frac{a}{A}\sqrt{2g} [t]_{0}^{T}$ $2(\sqrt{h} - \sqrt{H}) = -\frac{a}{A}\sqrt{2g} T$ $T = \frac{2A}{a\sqrt{2g}}(\sqrt{H} - \sqrt{h}) = \frac{A}{a}\sqrt{\frac{2}{g}}(\sqrt{H} - \sqrt{h})$