Question

Find the distance of direction image as Seen from

Answer 1

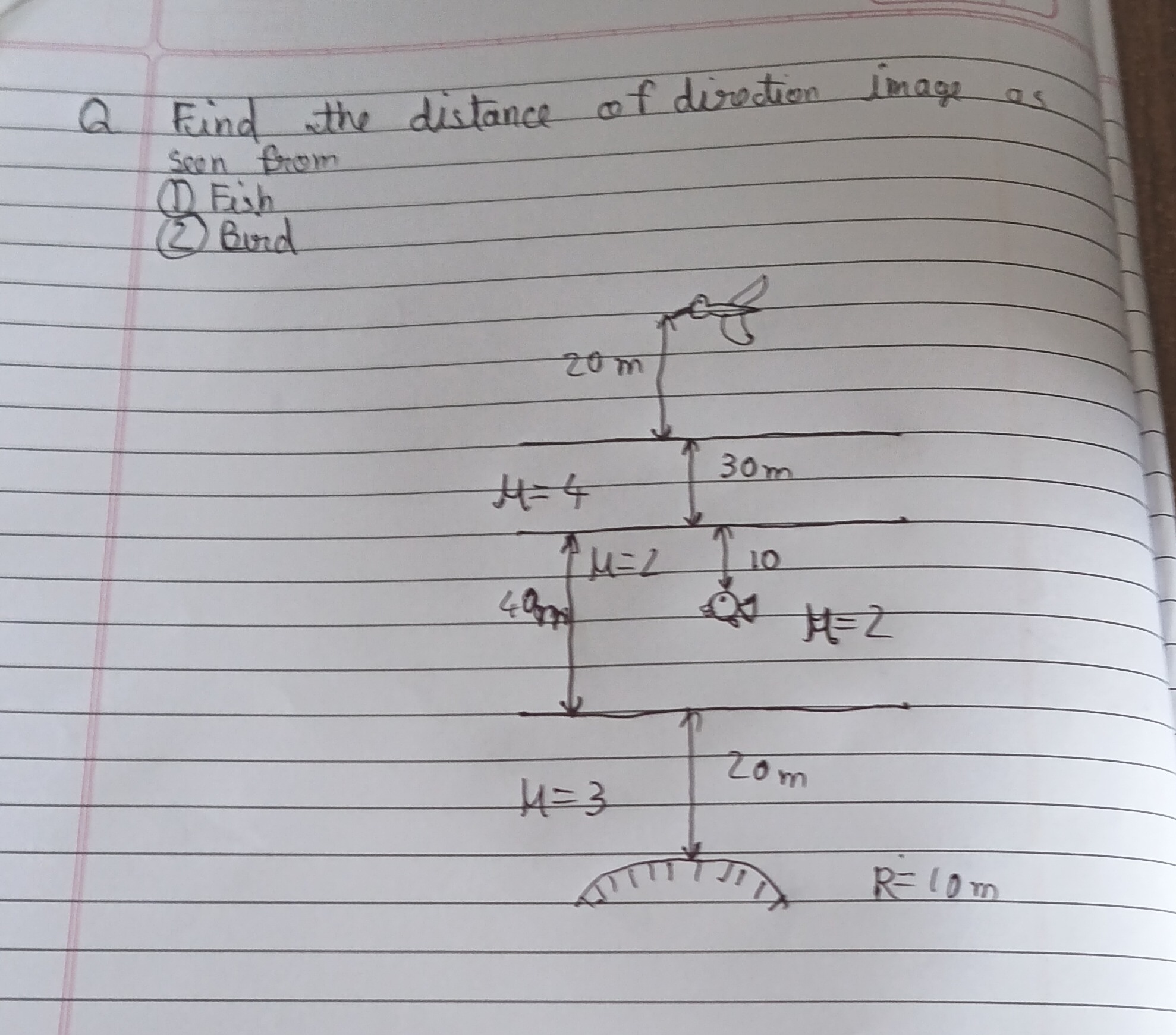
Fish: 34 m, Bird: 34.5 m

Answer 2

The problem involves calculating the apparent depth of an object when viewed through multiple layers of different refractive indices and a curved reflecting surface.

Assumptions and Setup:

1. The object is at the bottom, 20 m below the interface between medium $\mu_2$ and $\mu_3$.
2. The bottom surface is a concave mirror with a radius of curvature $R = -10$ m (concave upwards).
3. The refractive indices are given as $\mu_0 = 1$ (air), $\mu_1 = 4$, $\mu_2 = 2$, and $\mu_3$ (bottom medium).
4. The thicknesses of the layers are: $\mu_2$ is 40 m, $\mu_1$ is 30 m.
5. The fish is in medium $\mu_2$, 10 m above the interface between $\mu_1$ and $\mu_2$.
6. The bird is in air ($\mu_0$), 20 m above the interface between air and $\mu_1$.

Coordinate System: Let the interface between $\mu_2$ and $\mu_3$ (the mirror) be at $y=0$.

• Mirror: $y=0$, $R=-10$ m, $f = R/2 = -5$ m.
• Object: In $\mu_3$, 20 m below the mirror, so $y=-20$ m. Object distance $u = 20$ m.
• Interface $\mu_1-\mu_2$: Located 40 m above the mirror, so at $y=40$ m.
• Interface air-$\mu_1$: Located 30 m above the $\mu_1-\mu_2$ interface, so at $y=40+30=70$ m.
• Fish: In $\mu_2$, 10 m above the $\mu_1-\mu_2$ interface. So, $y = 40 - 10 = 30$ m.
• Bird: In air, 20 m above the air-$\mu_1$ interface. So, $y = 70 + 20 = 90$ m.

Step 1: Image formation by the mirror Using the mirror formula: $\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$ $\frac{1}{v} + \frac{1}{20} = \frac{1}{-5}$ $\frac{1}{v} = \frac{1}{-5} - \frac{1}{20} = \frac{-4 - 1}{20} = \frac{-5}{20} = -\frac{1}{4}$ $v = -4$ m. This image is formed 4 m in front of the mirror (on the side of $\mu_2$), so its position is $y=-4$ m. This is the real image formed by the mirror.

Step 2: Distance seen from the Fish The fish is at $y=30$ m. The real image is at $y=-4$ m. Both are in medium $\mu_2$ (or the image is in $\mu_2$). The distance of the image from the fish is $|30 - (-4)| = |30 + 4| = 34$ m.

Step 3: Distance seen from the Bird The real image is at $y=-4$ m in $\mu_2$. This image acts as an object for the layers above. The distance of this image from the interface $\mu_1-\mu_2$ (at $y=40$ m) is $d_{real} = 40 - (-4) = 44$ m. This object is in $\mu_2$ ($\mu_{object} = 2$).

3a. Apparent image in $\mu_1$ (viewed from $\mu_2$ to $\mu_1$) The observer is in $\mu_1$ ($\mu_{observer} = 4$). Using the apparent depth formula for a flat interface: $d_{apparent} = d_{real} \times \frac{\mu_{observer}}{\mu_{object}}$ $d'_{apparent} = 44 \times \frac{4}{2} = 44 \times 2 = 88$ m. This apparent image is formed 88 m above the interface $\mu_1-\mu_2$ (at $y=40$ m). Its position is $y = 40 + 88 = 128$ m. This image is in $\mu_1$.

3b. Apparent image in Air (viewed from $\mu_1$ to Air) Now, this image at $y=128$ m (in $\mu_1$) is viewed by the bird in air ($\mu_0=1$). The distance of this image from the interface air-$\mu_1$ (at $y=70$ m) is $d'_{real} = 128 - 70 = 58$ m. This object is in $\mu_1$ ($\mu_{object} = 4$). The observer is in air ($\mu_{observer} = 1$). Using the apparent depth formula: $d''_{apparent} = d'_{real} \times \frac{\mu_{observer}}{\mu_{object}}$ $d''_{apparent} = 58 \times \frac{1}{4} = \frac{58}{4} = 14.5$ m. This final apparent image is formed 14.5 m below the interface air-$\mu_1$ (at $y=70$ m). Its position is $y = 70 - 14.5 = 55.5$ m.

3c. Distance from the Bird The bird is at $y=90$ m. The final apparent image is at $y=55.5$ m. The distance of the apparent image from the bird is $|90 - 55.5| = 34.5$ m.

Summary:

• Distance of the image seen from the Fish: 34 m
• Distance of the image seen from the Bird: 34.5 m