Question
Question: Find point on parabola $\ast$ $(x-1)^2 = -12(y-2)$ with focal distance 6....
Find point on parabola ∗ (x−1)2=−12(y−2) with focal distance 6.
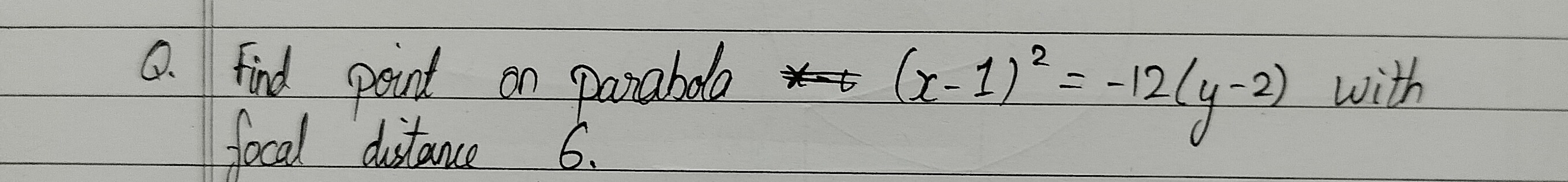
(7,−1) and (−5,−1)
(1,11) and (1,−1)
(7,11) and (−5,11)
(1,2)
The points on the parabola (x−1)2=−12(y−2) with a focal distance of 6 are (7,−1) and (−5,−1).
Solution
-
Identify Parabola Parameters: The given equation is (x−1)2=−12(y−2). This is in the standard form (x−h)2=4a(y−k), where (h,k) is the vertex.
- Vertex: (h,k)=(1,2).
- 4a=−12⟹a=−3.
- Since a is negative, the parabola opens downwards.
-
Determine Focus and Directrix:
- Focus: F=(h,k+a)=(1,2+(−3))=(1,−1).
- Directrix: y=k−a=2−(−3)=5.
-
Use the Definition of Focal Distance: The focal distance of a point P(x,y) on the parabola is the distance PF. We are given PF=6. By the definition of a parabola, the distance from any point on the parabola to the focus is equal to its distance to the directrix. Let PD be the distance from P(x,y) to the directrix y=5. So, PF=PD=∣y−5∣. Given PF=6, we have ∣y−5∣=6.
-
Solve for the y-coordinate: ∣y−5∣=6 implies two possibilities:
- y−5=6⟹y=11.
- y−5=−6⟹y=−1.
-
Check Validity of y-coordinates: The parabola opens downwards from its vertex (1,2), so all points on the parabola must satisfy y≤2.
- y=11 violates y≤2, so it's not a valid y-coordinate for a point on this parabola.
- y=−1 satisfies y≤2, so it's a valid y-coordinate.
-
Solve for the x-coordinate: Substitute y=−1 into the parabola's equation (x−1)2=−12(y−2): (x−1)2=−12(−1−2) (x−1)2=−12(−3) (x−1)2=36 Taking the square root of both sides: x−1=±6. This gives two possible x-values:
- x−1=6⟹x=7.
- x−1=−6⟹x=−5.
-
Identify the Points: The points on the parabola with focal distance 6 are (7,−1) and (−5,−1).
