Solveeit Logo
Login

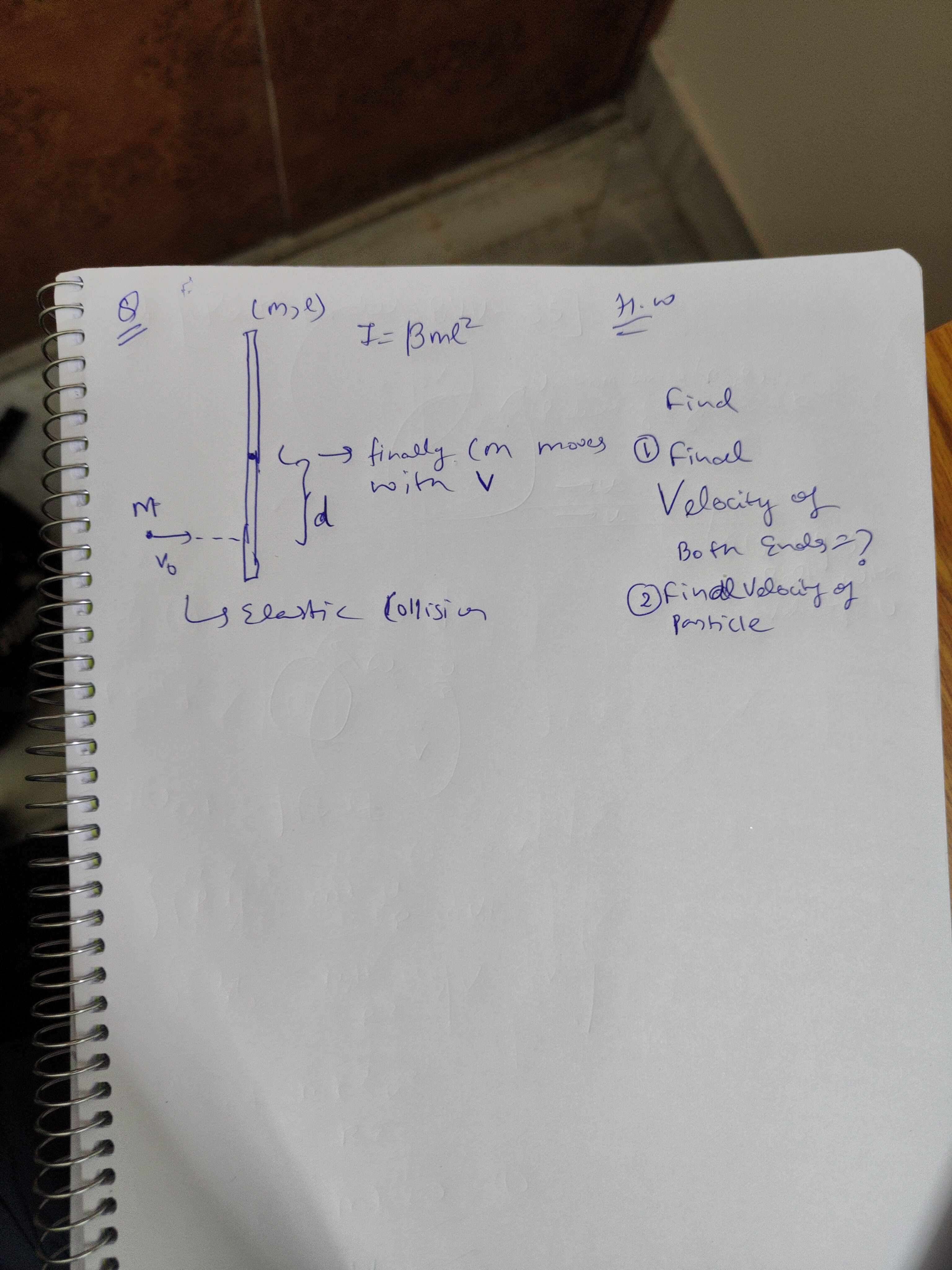
Question

Question: (m,l) $I= \beta ml^2$ H.w $\longrightarrow$ finally (m moves with V Find ① Final Velocity of Bot...

(m,l) I=βml2I= \beta ml^2

H.w

⟶\longrightarrow finally (m moves with V Find ① Final Velocity of Both Ends = ? ② Final Velocity of particle M V0V_0

⟶\longrightarrow Elastic Collision

Answer
  1. Final Velocity of both ends of the rod:
  • Top End: Vtop_end=2V0Mm(βl2+dl/2)(M+m)βml2+Mmd2V_{top\_end} = \frac{2 V_0 M m (\beta l^2 + d l/2)}{(M+m)\beta ml^2 + M m d^2}
  • Bottom End: Vbottom_end=2V0Mm(βl2−dl/2)(M+m)βml2+Mmd2V_{bottom\_end} = \frac{2 V_0 M m (\beta l^2 - d l/2)}{(M+m)\beta ml^2 + M m d^2}
  1. Final Velocity of particle M: VMf=V0[(M−m)βml2+Mmd2(M+m)βml2+Mmd2]V_{M_f} = V_0 \left[ \frac{(M-m)\beta ml^2 + M m d^2}{(M+m)\beta ml^2 + M m d^2} \right]
Explanation

Solution

The problem describes an elastic collision between a particle of mass M and initial velocity V₀ and a rod of mass m and length l. The rod is initially at rest. The collision occurs at a distance d from the center of mass (CM) of the rod. The moment of inertia of the rod about its CM is I = βml². We need to find the final velocity of both ends of the rod and the final velocity of the particle.

Let's define the velocities after the collision:

  • Final velocity of particle M: V_M_f
  • Final velocity of CM of rod m: V
  • Final angular velocity of rod m: ω_f

We will use the following conservation laws for an elastic collision:

  1. Conservation of Linear Momentum:

The total linear momentum of the system (particle + rod) is conserved. MV0+m(0)=MVMf+mVM V_0 + m(0) = M V_{M_f} + m V MV0=MVMf+mV(Equation 1)M V_0 = M V_{M_f} + m V \quad \text{(Equation 1)}

  1. Conservation of Angular Momentum:

The total angular momentum of the system about the CM of the rod is conserved. The initial angular momentum is due to the particle, and the final angular momentum is due to the particle's motion relative to the CM and the rod's rotation. (Assuming the collision point is d above the CM). MV0d=MVMfd+Iωf(Equation 2)M V_0 d = M V_{M_f} d + I \omega_f \quad \text{(Equation 2)}

  1. Coefficient of Restitution (e=1 for elastic collision):

The relative velocity of separation along the line of impact is equal to the negative of the relative velocity of approach. The velocity of the point of impact on the rod just before collision is 0. The velocity of the point of impact on the rod just after collision is V + ω_f d. e=(V+ωfd)−VMfV0−0=1e = \frac{(V + \omega_f d) - V_{M_f}}{V_0 - 0} = 1 V0=V+ωfd−VMf(Equation 3)V_0 = V + \omega_f d - V_{M_f} \quad \text{(Equation 3)}

Now we solve these three equations for V_M_f, V, and ω_f.

From Equation 1: VMf=V0−mMV(Equation 4)V_{M_f} = V_0 - \frac{m}{M}V \quad \text{(Equation 4)}

Substitute Equation 4 into Equation 3: V0=V+ωfd−(V0−mMV)V_0 = V + \omega_f d - \left(V_0 - \frac{m}{M}V\right) 2V0=V(1+mM)+ωfd2V_0 = V \left(1 + \frac{m}{M}\right) + \omega_f d 2V0=V(M+mM)+ωfd(Equation 5)2V_0 = V \left(\frac{M+m}{M}\right) + \omega_f d \quad \text{(Equation 5)}

Substitute Equation 4 into Equation 2: MV0d=M(V0−mMV)d+IωfM V_0 d = M \left(V_0 - \frac{m}{M}V\right) d + I \omega_f MV0d=MV0d−mVd+IωfM V_0 d = M V_0 d - m V d + I \omega_f 0=−mVd+Iωf0 = -m V d + I \omega_f Iωf=mVdI \omega_f = m V d ωf=mVdI(Equation 6)\omega_f = \frac{m V d}{I} \quad \text{(Equation 6)}

Now substitute Equation 6 into Equation 5: 2V0=V(M+mM)+(mVdI)d2V_0 = V \left(\frac{M+m}{M}\right) + \left(\frac{m V d}{I}\right) d 2V0=V[M+mM+md2I]2V_0 = V \left[ \frac{M+m}{M} + \frac{m d^2}{I} \right] 2V0=V[(M+m)I+Mmd2MI]2V_0 = V \left[ \frac{(M+m)I + M m d^2}{M I} \right]

Solving for V (final velocity of CM of rod): V=2V0MI(M+m)I+Mmd2V = \frac{2 V_0 M I}{(M+m)I + M m d^2}

Now substitute V back into Equation 6 to find ω_f: ωf=mdI[2V0MI(M+m)I+Mmd2]\omega_f = \frac{m d}{I} \left[ \frac{2 V_0 M I}{(M+m)I + M m d^2} \right] ωf=2V0Mmd(M+m)I+Mmd2\omega_f = \frac{2 V_0 M m d}{(M+m)I + M m d^2}

Finally, substitute V back into Equation 4 to find V_M_f (final velocity of particle): VMf=V0−mM[2V0MI(M+m)I+Mmd2]V_{M_f} = V_0 - \frac{m}{M} \left[ \frac{2 V_0 M I}{(M+m)I + M m d^2} \right] VMf=V0[1−2mI(M+m)I+Mmd2]V_{M_f} = V_0 \left[ 1 - \frac{2 m I}{(M+m)I + M m d^2} \right] VMf=V0[(M+m)I+Mmd2−2mI(M+m)I+Mmd2]V_{M_f} = V_0 \left[ \frac{(M+m)I + M m d^2 - 2 m I}{(M+m)I + M m d^2} \right] VMf=V0[MI+mI+Mmd2−2mI(M+m)I+Mmd2]V_{M_f} = V_0 \left[ \frac{M I + m I + M m d^2 - 2 m I}{(M+m)I + M m d^2} \right] VMf=V0[(M−m)I+Mmd2(M+m)I+Mmd2]V_{M_f} = V_0 \left[ \frac{(M-m)I + M m d^2}{(M+m)I + M m d^2} \right]

The problem states I = βml². Let's substitute this into the expressions. Let K = (M+m)I + M m d^2 = (M+m)βml^2 + M m d^2.

So, the final velocities are:

  1. Final Velocity of particle M: VMf=V0[(M−m)βml2+Mmd2(M+m)βml2+Mmd2]V_{M_f} = V_0 \left[ \frac{(M-m)\beta ml^2 + M m d^2}{(M+m)\beta ml^2 + M m d^2} \right]

  2. Final Velocity of CM of rod: V=2V0Mβml2(M+m)βml2+Mmd2V = \frac{2 V_0 M \beta ml^2}{(M+m)\beta ml^2 + M m d^2}

  3. Final Angular Velocity of rod: ωf=2V0Mmd(M+m)βml2+Mmd2\omega_f = \frac{2 V_0 M m d}{(M+m)\beta ml^2 + M m d^2}

Now, let's find the final velocity of both ends of the rod. The velocity of any point on the rod at a distance y from the CM is given by V_point = V + ω_f y. The top end is at y = +l/2 and the bottom end is at y = -l/2.

Velocity of the top end (V_top_end): Vtop_end=V+ωf(l2)V_{top\_end} = V + \omega_f \left(\frac{l}{2}\right) Vtop_end=2V0Mβml2K+2V0MmdK(l2)V_{top\_end} = \frac{2 V_0 M \beta ml^2}{K} + \frac{2 V_0 M m d}{K} \left(\frac{l}{2}\right) Vtop_end=2V0Mm(βl2+dl/2)KV_{top\_end} = \frac{2 V_0 M m (\beta l^2 + d l/2)}{K} Vtop_end=2V0Mm(βl2+dl/2)(M+m)βml2+Mmd2V_{top\_end} = \frac{2 V_0 M m (\beta l^2 + d l/2)}{(M+m)\beta ml^2 + M m d^2}

Velocity of the bottom end (V_bottom_end): Vbottom_end=V+ωf(−l2)V_{bottom\_end} = V + \omega_f \left(-\frac{l}{2}\right) Vbottom_end=2V0Mβml2K−2V0MmdK(l2)V_{bottom\_end} = \frac{2 V_0 M \beta ml^2}{K} - \frac{2 V_0 M m d}{K} \left(\frac{l}{2}\right) Vbottom_end=2V0Mm(βl2−dl/2)KV_{bottom\_end} = \frac{2 V_0 M m (\beta l^2 - d l/2)}{K} Vbottom_end=2V0Mm(βl2−dl/2)(M+m)βml2+Mmd2V_{bottom\_end} = \frac{2 V_0 M m (\beta l^2 - d l/2)}{(M+m)\beta ml^2 + M m d^2}

Summary of Final Velocities:

  1. Final Velocity of both ends of the rod:
  • Top End: Vtop_end=2V0Mm(βl2+dl/2)(M+m)βml2+Mmd2V_{top\_end} = \frac{2 V_0 M m (\beta l^2 + d l/2)}{(M+m)\beta ml^2 + M m d^2}
  • Bottom End: Vbottom_end=2V0Mm(βl2−dl/2)(M+m)βml2+Mmd2V_{bottom\_end} = \frac{2 V_0 M m (\beta l^2 - d l/2)}{(M+m)\beta ml^2 + M m d^2}
  1. Final Velocity of particle M: VMf=V0[(M−m)βml2+Mmd2(M+m)βml2+Mmd2]V_{M_f} = V_0 \left[ \frac{(M-m)\beta ml^2 + M m d^2}{(M+m)\beta ml^2 + M m d^2} \right]

The problem is solved using the principles of conservation of linear momentum, conservation of angular momentum, and the definition of the coefficient of restitution for an elastic collision.

  1. Conservation of Linear Momentum: Relates the initial and final linear momenta of the particle and the rod's center of mass.
  2. Conservation of Angular Momentum: Relates the initial and final angular momenta of the system about the center of mass of the rod. The angular momentum of the particle is M V d and the rod's angular momentum is Iω.
  3. Coefficient of Restitution (e=1): For an elastic collision, the relative speed of separation between the colliding surfaces is equal to the relative speed of approach. This provides a third independent equation.

These three equations are then solved simultaneously to find the three unknowns: the final velocity of the particle (V_M_f), the final velocity of the rod's center of mass (V), and the final angular velocity of the rod (ω_f). Finally, the velocities of the ends of the rod are determined by combining the translational velocity of the CM and the rotational velocity component (V_point = V + ωy).