Question
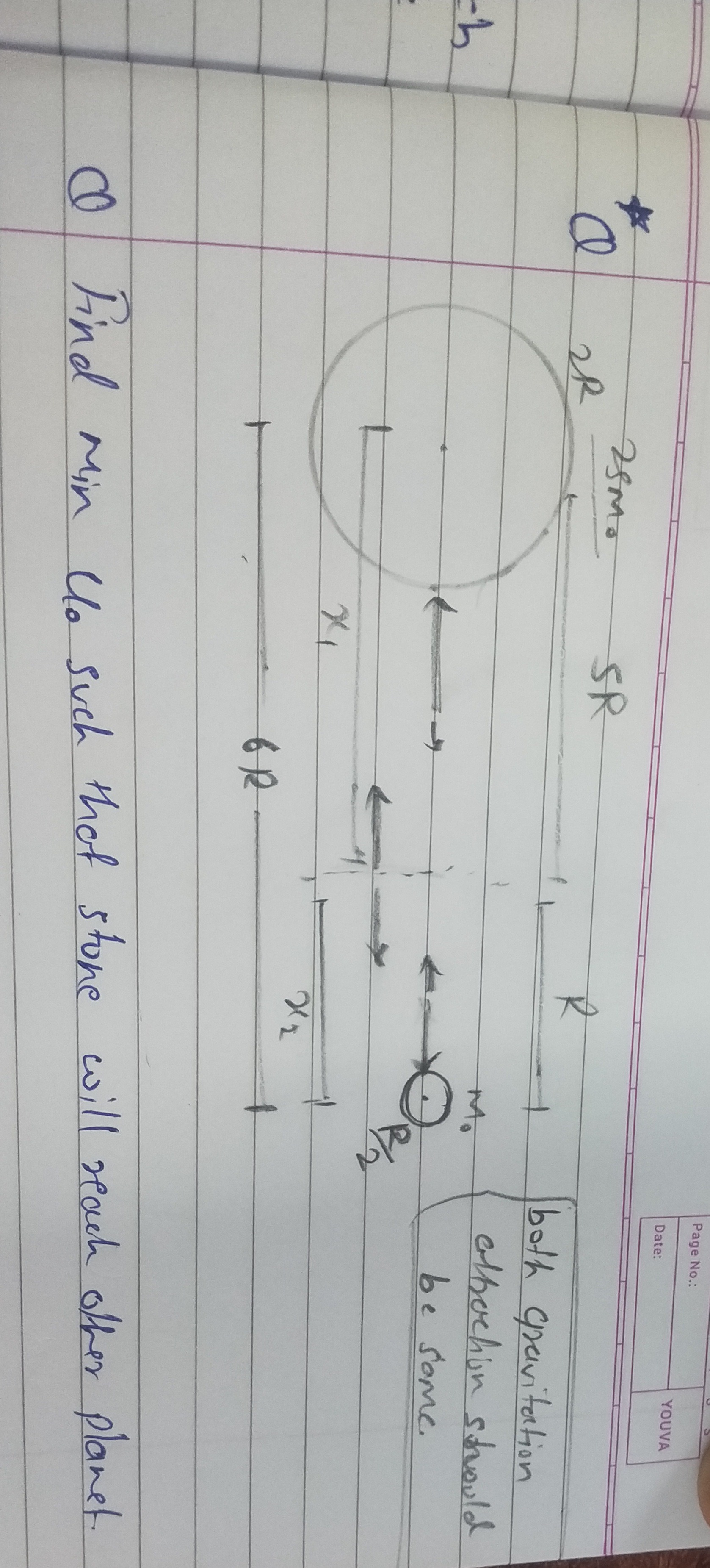
Question: Find min $U_0$ such that stone will reach other planet....
Find min U0 such that stone will reach other planet.
12R5GMm0(21−45)
Solution
The minimum initial kinetic energy U0 is found by setting the total initial energy (kinetic + potential) equal to the potential energy at the neutral point, which is the peak of the gravitational potential barrier.
-
Locate the neutral point: The neutral point is where the gravitational forces from the two planets balance. Let x1 be the distance from Planet 1 (mass 25M) and x2 be the distance from Planet 2 (mass 5M). The distance between centers is 6R. x12G(25M)m0=x22G(5M)m0⟹5x2=x1 Given x1+x2=6R, we find x1=23R(5−5) and x2=23R(5−1).
-
Calculate potential energy at the neutral point (Uneutral): Uneutral=−x1G(25M)m0−x2G(5M)m0=−3R5GMm0(3+5)
-
Calculate initial potential energy (Uinitial): The stone starts at the surface of Planet 1 (distance 2R from its center) and is 4R from the center of Planet 2. Uinitial=−2RG(25M)m0−4RG(5M)m0=−4R55GMm0
-
Find minimum U0: For the stone to reach the neutral point, U0+Uinitial≥Uneutral. The minimum U0 occurs when U0+Uinitial=Uneutral. U0=Uneutral−Uinitial=−3R5GMm0(3+5)−(−4R55GMm0) U0=12RGMm0(165−20(3+5))=12R5GMm0(21−45)
