Question
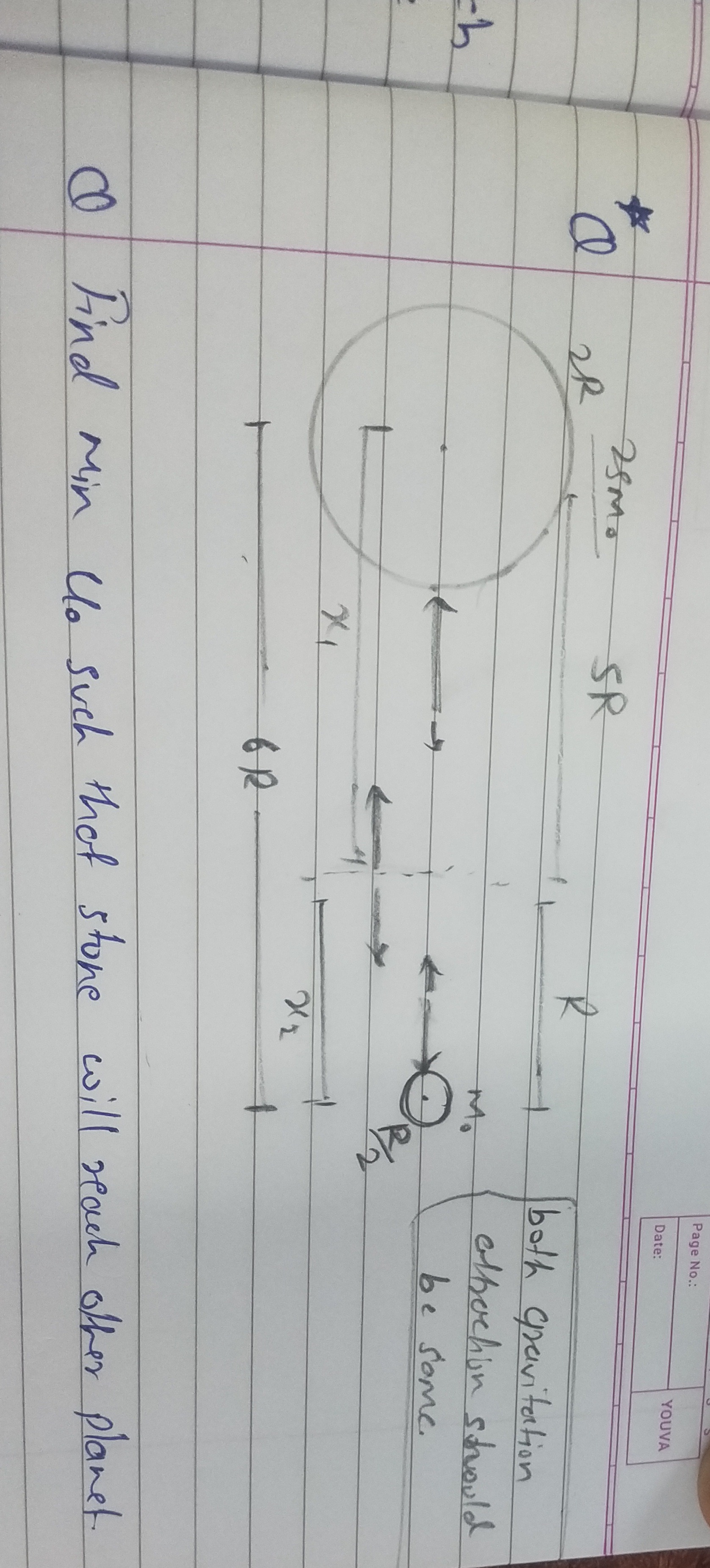
Question: Find min $U_0$ such that stone will reach other planet....
Find min U0 such that stone will reach other planet.
415RGMm0
Solution
The stone needs to be launched from the surface of the larger planet (mass 25M, radius 2R) with sufficient initial kinetic energy U0 to reach the surface of the smaller planet (mass 5M, radius R). The distance between the centers of the planets is 6R.
-
Initial State: The stone is launched from the surface of the larger planet. Its initial distance from the center of the larger planet is ri=2R. Its initial distance from the center of the smaller planet is 6R−2R=4R. The initial kinetic energy is U0. The initial potential energy Vi due to both planets is: Vi=−2RG(25M)m0−4RG(5M)m0=−455RGMm0
-
Final State: The stone reaches the surface of the smaller planet. Its final distance from the center of the smaller planet is rf=R. Its final distance from the center of the larger planet is 6R−R=5R. For the minimum initial kinetic energy, the stone reaches the destination with zero final kinetic energy (Kf=0). The final potential energy Vf at the surface of the smaller planet is: Vf=−5RG(25M)m0−RG(5M)m0=−10RGMm0
-
Conservation of Energy: Ki+Vi=Kf+Vf⟹U0+Vi=0+Vf⟹U0=Vf−Vi U0=(−10RGMm0)−(−455RGMm0)=415RGMm0
