Question
Question: Effective capacitance between A and B in the figure shown below is ?...
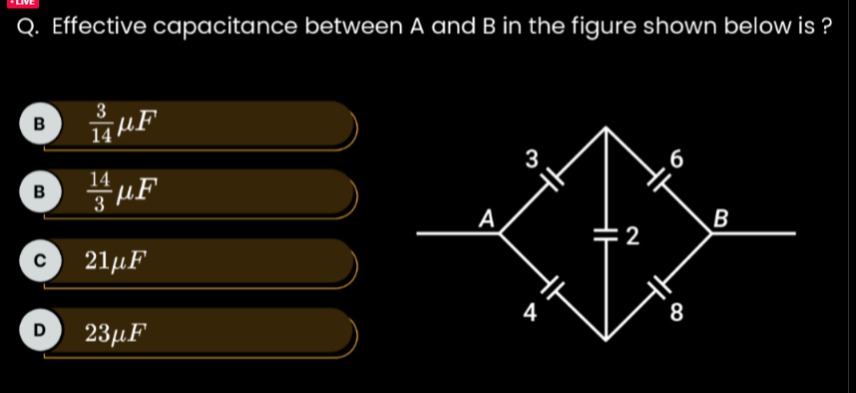
Effective capacitance between A and B in the figure shown below is ?
143μF
314μF
21μF
23μF
314μF
Solution
The given circuit is a Wheatstone bridge configuration of capacitors. Let the capacitors be denoted as follows:
C1=3μF (between A and the top node) C2=6μF (between the top node and B) C3=4μF (between A and the bottom node) C4=8μF (between the bottom node and B) C5=2μF (between the top node and the bottom node)
In a Wheatstone bridge with capacitors, the bridge is balanced if the ratio of capacitances in adjacent arms is equal, i.e., C3C1=C4C2.
Let's check the condition for the given values: C3C1=43 C4C2=86=43
Since C3C1=C4C2, the Wheatstone bridge is balanced.
When the bridge is balanced, the potential difference across the capacitor in the middle arm (C5) is zero. Therefore, no charge flows through or accumulates on the capacitor C5, and it can be removed from the circuit without affecting the effective capacitance between A and B.
After removing C5, the circuit simplifies to two parallel branches. The top branch consists of C1 and C2 in series, and the bottom branch consists of C3 and C4 in series. These two series combinations are connected in parallel between A and B.
The equivalent capacitance of C1 and C2 in series is Cseries1=C1+C2C1C2. Cseries1=3+63×6=918=2μF.
The equivalent capacitance of C3 and C4 in series is Cseries2=C3+C4C3C4. Cseries2=4+84×8=1232=38μF.
The effective capacitance between A and B is the parallel combination of Cseries1 and Cseries2. CAB=Cseries1+Cseries2. CAB=2+38=36+38=36+8=314μF.
The effective capacitance between A and B is 314μF.
