Question
Question: Calculate $E_{Cu^{+2}/Cu}$ at $pH=14$; given that $K_{sp}$ of $Cu(OH)_2 = 10^{-19}$; $E_{Cu^{+2}/Cu}...
Calculate ECu+2/Cu at pH=14; given that Ksp of Cu(OH)2=10−19; ECu+2/Cu∘=0.034V at 298K.
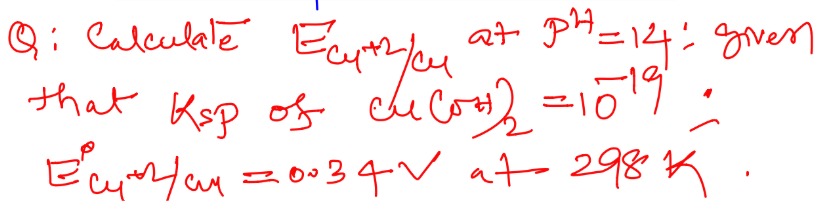
-0.22 V
Solution
To calculate the reduction potential ECu+2/Cu at pH=14, we need to determine the concentration of Cu2+ ions under these conditions and then apply the Nernst equation.
1. Determine [OH−] from pH: Given pH = 14. At 298 K, pH + pOH = 14. So, pOH = 14 - pH = 14 - 14 = 0. Therefore, the concentration of hydroxide ions is [OH−]=10−pOH=100=1 M.
2. Determine [Cu2+] from Ksp: The dissolution equilibrium for copper(II) hydroxide is: Cu(OH)2(s)⇌Cu2+(aq)+2OH−(aq) The solubility product constant (Ksp) is given by: Ksp=[Cu2+][OH−]2 Given Ksp of Cu(OH)2=10−19 and we found [OH−]=1 M. 10−19=[Cu2+](1)2 [Cu2+]=10−19 M
3. Apply the Nernst Equation: The half-cell reaction for the copper couple is: Cu2+(aq)+2e−→Cu(s) The Nernst equation for this reaction at 298 K is: ECu2+/Cu=ECu2+/Cu∘−n0.059log[Cu2+]1 Here, n=2 (number of electrons transferred).
Note on ECu+2/Cu∘: The question states ECu+2/Cu∘=0.034V. However, the standard reduction potential for Cu2+/Cu is commonly accepted as +0.34 V. The similar question also uses +0.34 V and leads to a standard result. Assuming the given value 0.034V is a typo and should be 0.34V to align with standard values and typical problem expectations:
Using ECu2+/Cu∘=0.34 V: ECu2+/Cu=0.34−20.059log10−191 ECu2+/Cu=0.34−20.059log(1019) ECu2+/Cu=0.34−(0.0295×19) ECu2+/Cu=0.34−0.5605 ECu2+/Cu=−0.2205 V
Rounding to two decimal places, ECu2+/Cu=−0.22 V.
If we strictly use the value given in the question, ECu+2/Cu∘=0.034V: ECu2+/Cu=0.034−20.059×19 ECu2+/Cu=0.034−0.5605 ECu2+/Cu=−0.5265 V
Given the context of similar problems and standard values, it is highly probable that ECu+2/Cu∘=0.34V was intended. Therefore, we proceed with the result obtained using 0.34V.
The final answer is −0.22V.
Explanation of the solution:
- Calculate [OH−] from pH=14: pOH = 0, so [OH−]=1 M.
- Calculate [Cu2+] from Ksp=[Cu2+][OH−]2: [Cu2+]=Ksp/[OH−]2=10−19/(1)2=10−19 M.
- Apply Nernst equation: ECu2+/Cu=ECu2+/Cu∘−20.059log[Cu2+]1. Using ECu2+/Cu∘=0.34V (assuming typo correction from 0.034V): ECu2+/Cu=0.34−20.059log(1019)=0.34−0.0295×19=0.34−0.5605=−0.2205V.
Answer:
The calculated ECu+2/Cu at pH=14 is -0.22 V.
