Question

Area of the region bounded between $y = x^3 - 5x^2 + 6x$ and the $x$-axis is ______

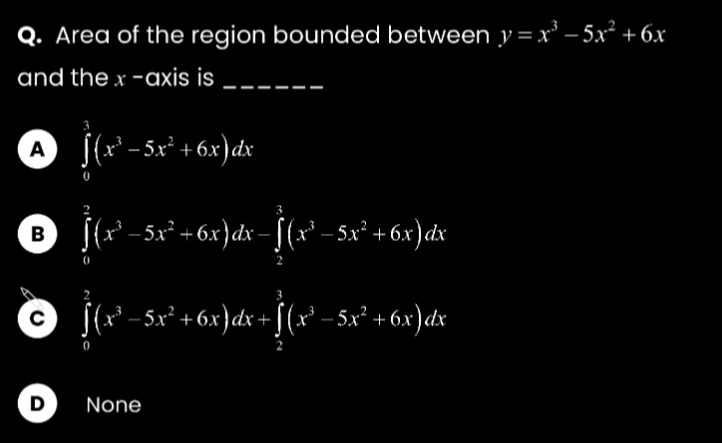
• A. $\int_{0}^{3}(x^3 - 5x^2 + 6x)dx$
• B. $\int_{0}^{2}(x^3 - 5x^2 + 6x)dx - \int_{2}^{3}(x^3 - 5x^2 + 6x)dx$
• C. $\int_{0}^{2}(x^3 - 5x^2 + 6x)dx + \int_{2}^{3}(x^3 - 5x^2 + 6x)dx$
• D. None

Answer 1

Answer: (B)

B

Answer 2

To find the area of the region bounded between the curve $y = x^3 - 5x^2 + 6x$ and the x-axis, we first need to find the points where the curve intersects the x-axis. These points are the roots of the equation $y=0$.

Set $y=0$: $x^3 - 5x^2 + 6x = 0$ Factor out $x$: $x(x^2 - 5x + 6) = 0$ Factor the quadratic expression: $x(x-2)(x-3) = 0$ The x-intercepts are $x=0$, $x=2$, and $x=3$. These points define the intervals over which we need to integrate. The relevant intervals are $(0, 2)$ and $(2, 3)$.

Next, we need to determine the sign of the function $y = x^3 - 5x^2 + 6x$ in each interval.

1. Interval (0, 2):
   Choose a test point, for example, $x=1$.
   $y(1) = 1^3 - 5(1)^2 + 6(1) = 1 - 5 + 6 = 2$.
   Since $y(1) > 0$, the curve is above the x-axis in the interval $(0, 2)$.
   The area in this interval is given by $\int_{0}^{2} (x^3 - 5x^2 + 6x) dx$.

2. Interval (2, 3):
   Choose a test point, for example, $x=2.5$.
   $y(2.5) = (2.5)^3 - 5(2.5)^2 + 6(2.5)$
   $= 15.625 - 5(6.25) + 15$
   $= 15.625 - 31.25 + 15$
   $= -0.625$.
   Since $y(2.5) < 0$, the curve is below the x-axis in the interval $(2, 3)$.
   To find the area when the curve is below the x-axis, we take the absolute value of the integral.
   The area in this interval is given by $\left| \int_{2}^{3} (x^3 - 5x^2 + 6x) dx \right|$. Since the integral itself will yield a negative value, taking its absolute value means multiplying by -1.
   So, the area is $-\int_{2}^{3} (x^3 - 5x^2 + 6x) dx$.

The total area bounded by the curve and the x-axis is the sum of the areas from these two intervals:
Total Area = $\int_{0}^{2} (x^3 - 5x^2 + 6x) dx + \left( -\int_{2}^{3} (x^3 - 5x^2 + 6x) dx \right)$
Total Area = $\int_{0}^{2} (x^3 - 5x^2 + 6x) dx - \int_{2}^{3} (x^3 - 5x^2 + 6x) dx$

Thus, the correct answer is B.