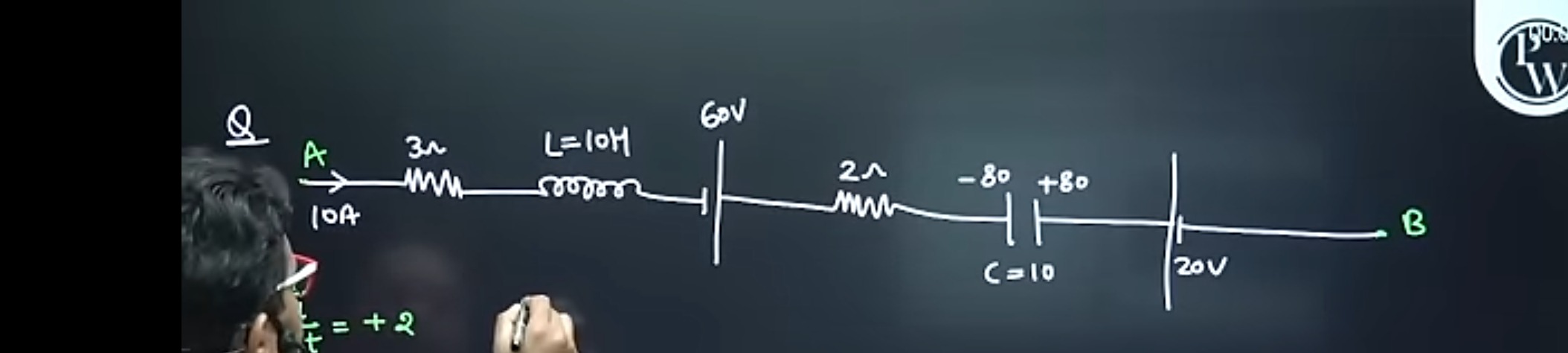
Question

A

3$\Omega$ L=10H 60V

2$\Omega$ -80 +80 B C=10 20V 10A $\frac{d}{t}=+2$

Answer 1

-18V

Answer 2

To find the potential difference $V_A - V_B$, we can traverse the circuit from point A to point B and sum the potential changes across each component.

Let's denote the potential at point A as $V_A$. We move from A to B.

1. Across the $3\Omega$ resistor: Current $I = 10A$ flows from A to B. Potential drops across a resistor in the direction of current. Potential change = $-I \times R_1 = -10A \times 3\Omega = -30V$.

2. Across the $L=10H$ inductor: The current is increasing, $\frac{dI}{dt} = +2 A/s$. An inductor opposes the change in current. Since the current is increasing in the direction of travel, the inductor creates a back EMF that opposes this increase, causing a potential drop. Potential change = $-L \frac{dI}{dt} = -10H \times 2 A/s = -20V$.

3. Across the $60V$ voltage source: The standard convention for a DC voltage source symbol is that the longer line is the positive terminal and the shorter line is the negative terminal. Moving from A to B, we encounter the negative terminal first and then the positive terminal. Therefore, there is a potential gain. Potential change = $+60V$.

4. Across the $2\Omega$ resistor: Current $I = 10A$ flows from A to B. Potential drops across a resistor in the direction of current. Potential change = $-I \times R_2 = -10A \times 2\Omega = -20V$.

5. Across the capacitor ($C=10$ with charges -80 and +80): The plate with +80 charge is at a higher potential than the plate with -80 charge. Moving from A to B, we move from the negative plate (-80) to the positive plate (+80). Therefore, there is a potential gain. The potential difference across the capacitor is $V_C = \frac{Q}{C} = \frac{80}{10} = 8V$. Potential change = $+8V$.

6. Across the $20V$ voltage source: Similar to the $60V$ source, moving from A to B, we encounter the negative terminal first and then the positive terminal. Therefore, there is a potential gain. Potential change = $+20V$.

Now, sum all the potential changes starting from $V_A$ to reach $V_B$: $V_A - 30V - 20V + 60V - 20V + 8V + 20V = V_B$

Combine the terms: $V_A - (30 + 20 + 20) + (60 + 8 + 20) = V_B$ $V_A - 70 + 88 = V_B$ $V_A + 18 = V_B$

To find $V_A - V_B$: $V_A - V_B = -18V$

The final answer is $\boxed{-18V}$.

Explanation of the solution: The potential difference $V_A - V_B$ is calculated by traversing the circuit from A to B, summing potential changes. Potential drops across resistors ($IR$) and inductors ($L \frac{dI}{dt}$) when current flows in the direction of traversal or increases. Potential increases across voltage sources when moving from negative to positive terminals. Potential increases across capacitors when moving from the negatively charged plate to the positively charged plate ($Q/C$). Applying these rules: $V_A - (10 \times 3) - (10 \times 2) + 60 - (10 \times 2) + (80/10) + 20 = V_B$ $V_A - 30 - 20 + 60 - 20 + 8 + 20 = V_B$ $V_A + 18 = V_B$ $V_A - V_B = -18V$