Question

Four small blocks are interconnected with light strings and placed over a fixed sphere as shown. Blocks A, B and C are identical each having mass m = 1 kg. Block D has a mass of m' = 2 kg. The coefficient of friction between the blocks and the sphere is µ = 0.5. The system is released from the position shown in figure.

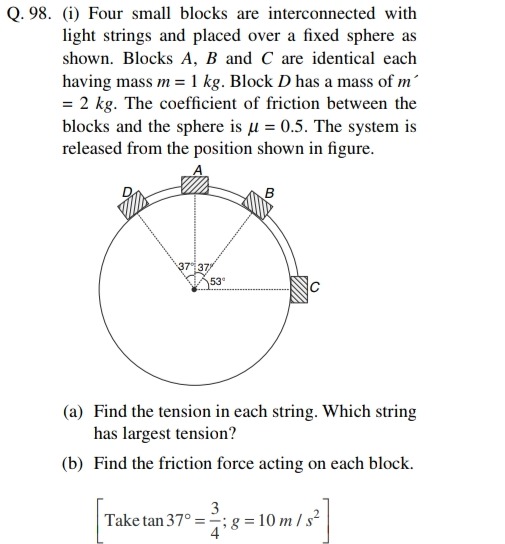
• A. (a) Find the tension in each string. Which string has largest tension?
• B. (b) Find the friction force acting on each block.

Answer 1

The problem statement contains inconsistencies that prevent a valid calculation of tensions and friction forces. Specifically, assuming the system moves with acceleration, the equations of motion lead to negative tensions, indicating a flaw in the problem's parameters or setup.

Answer 2

The problem involves analyzing forces on interconnected blocks on a sphere. The tangential components of gravity, normal forces, friction, and tensions in the strings need to be considered. Let's denote the angle of a block from the upward vertical as $\theta$. The tangential component of gravity is $mg \sin \theta$, and the normal force is $N = mg \cos \theta$. The kinetic friction force is $f = \mu N = \mu mg \cos \theta$.

The angles from the upward vertical are given or can be inferred: Block A: $\theta_A = 0^\circ$ Block D: $\theta_D = 37^\circ$ Block B: $\theta_B = 37^\circ$ Block C: $\theta_C = 90^\circ$ (assuming it's at the horizontal position relative to A and D, and B is at the same level as D)

Masses: $m_A = m_B = m_C = m = 1$ kg. $m_D = m' = 2$ kg. Given $\mu = 0.5$, $\tan 37^\circ = 3/4$, so $\sin 37^\circ = 3/5$ and $\cos 37^\circ = 4/5$. $g = 10 \, m/s^2$.

The angles of the strings with the tangential direction need to be calculated. Let $\alpha$ be the angle of string DA (and AB) with the tangential direction at A (and D, B). Let $\beta$ be the angle of string BC with the tangential direction at B (and C). From geometric considerations (using the law of cosines on the triangle formed by the center of the sphere and two adjacent blocks), the angle $\alpha \approx 18.43^\circ$ and $\cos \alpha = 3/\sqrt{10}$. The angle $\beta \approx 26.5^\circ$ and $\cos \beta = 2/\sqrt{5}$.

Assuming the system moves with a common tangential acceleration $a$: Friction forces: $f_A = \mu m g \cos 0^\circ = 0.5 \times 1 \times 10 \times 1 = 5$ N. $f_D = \mu m g \cos 37^\circ = 0.5 \times 1 \times 10 \times (4/5) = 4$ N. $f_B = \mu m g \cos 37^\circ = 0.5 \times 1 \times 10 \times (4/5) = 4$ N. $f_C = \mu m' g \cos 90^\circ = 0.5 \times 2 \times 10 \times 0 = 0$ N.

Equations of motion in the tangential direction: Block A: $mg \sin 0^\circ - f_A - T_{DA} \cos \alpha - T_{AB} \cos \alpha = m a$ $0 - 5 - T_1 \cos \alpha - T_1 \cos \alpha = a \implies -5 - 2 T_1 \cos \alpha = a$ (Equation 1)

Block D: $mg \sin 37^\circ - f_D - T_{DA} \cos \alpha = m a$ $1 \times 10 \times (3/5) - 4 - T_1 \cos \alpha = a \implies 6 - 4 - T_1 \cos \alpha = a \implies 2 - T_1 \cos \alpha = a$ (Equation 2)

Equating expressions for $a$ from Equation 1 and Equation 2: $-5 - 2 T_1 \cos \alpha = 2 - T_1 \cos \alpha$ $-7 = T_1 \cos \alpha$

Since $\cos \alpha$ is positive, this implies $T_1$ (tension in string DA/AB) must be negative, which is physically impossible. This inconsistency suggests an error in the problem statement, the provided diagram, or the given parameters. Without a valid set of parameters or a corrected setup, it is impossible to determine the tensions and friction forces accurately.

However, considering the forces involved, block C has the largest tangential component of gravity ($m'g = 20$ N) and zero friction, making it the most likely block to drive the motion. Therefore, the string connected to block C ($T_{BC}$) is expected to have the largest tension.