Question

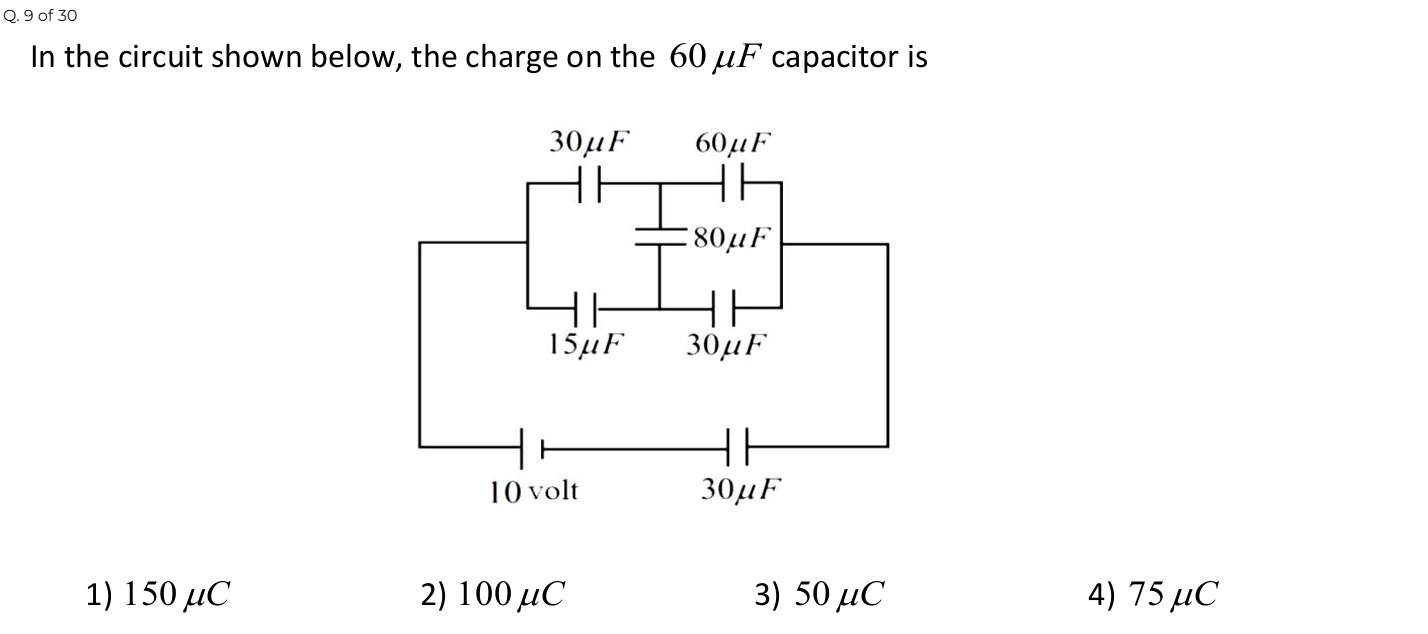
In the circuit shown below, the charge on the 60 μF capacitor is

• A. 150 μC
• B. 100 μC
• C. 50 μC
• D. 75 μC

Answer 1

Answer: (A)

150 μC

Answer 2

Step 1: Identify the bridge network and check balance
We have two series branches between the same nodes:

• Top branch: 30 μF – 60 μF
• Bottom branch: 15 μF – 30 μF
  With a central 80 μF between the junctions.
  The bridge is balanced if

$$\frac{C_{1}}{C_{3}} \;=\;\frac{C_{2}}{C_{4}} \quad\Longrightarrow\quad \frac{30}{15} \;=\;\frac{60}{30} \;=\;2$$

Hence no current (charge) flows through the 80 μF, so it can be removed.

Step 2: Reduce each series branch
Top branch equivalent:

$$C_{t} = \frac{30\times60}{30+60} = 20\;\mu\text{F}$$

Bottom branch equivalent:

$$C_{b} = \frac{15\times30}{15+30} = 10\;\mu\text{F}$$

Step 3: Parallel combination of the two reduced branches

$$C_{\text{net}} = C_{t} + C_{b} = 20+10 = 30\;\mu\text{F}$$

Step 4: Series with the bottom 30 μF capacitor and the 10 V source
Total series capacitance:

$$C_{\text{eq}} = \frac{30\times30}{30+30} = 15\;\mu\text{F}$$

Charge on each series element:

$$Q = C_{\text{eq}}\times V = 15\;\mu\text{F}\times10\;\text{V} = 150\;\mu\text{C}$$

Since the 60 μF capacitor is in series in the top branch, it carries the same charge:

$$\boxed{Q_{60} = 150\;\mu\text{C}}$$