Solveeit Logo
Login

Question

Question: \(\log_{27}32 \cdot \log_{49}625 \cdot \log_{0.5}7^{-1} \cdot \log_{125}81 = ?\)...

log⁡2732⋅log⁡49625⋅log⁡0.57−1⋅log⁡12581=?\log_{27}32 \cdot \log_{49}625 \cdot \log_{0.5}7^{-1} \cdot \log_{125}81 = ?

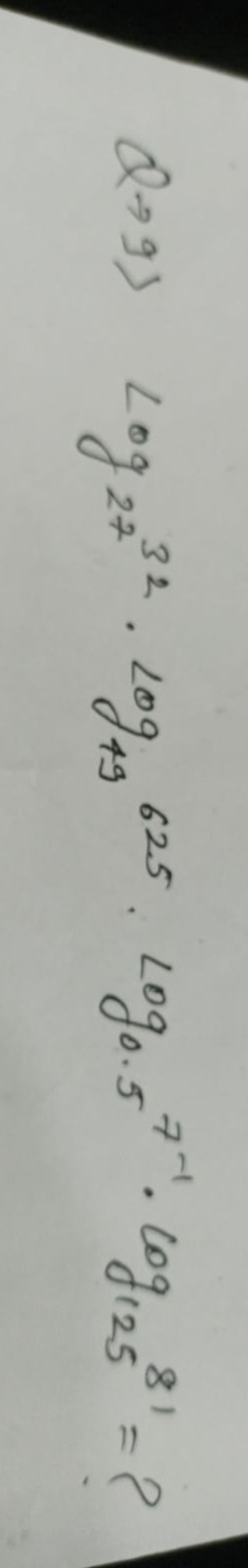
Answer

409\displaystyle \frac{40}{9}

Explanation

Solution

We apply the change of base formula and simplify:

  1. log⁡2732=ln⁡32ln⁡27=5ln⁡23ln⁡3\log_{27}32 = \frac{\ln 32}{\ln 27} = \frac{5\ln 2}{3\ln 3}

  2. log⁡49625=ln⁡625ln⁡49=4ln⁡52ln⁡7=2ln⁡5ln⁡7\log_{49}625 = \frac{\ln 625}{\ln 49} = \frac{4\ln 5}{2\ln 7} = \frac{2\ln 5}{\ln 7}

  3. log⁡0.57−1=ln⁡(7−1)ln⁡(0.5)=−ln⁡7−ln⁡2=ln⁡7ln⁡2\log_{0.5}7^{-1} = \frac{\ln(7^{-1})}{\ln(0.5)} = \frac{-\ln 7}{-\ln 2} = \frac{\ln 7}{\ln 2}

  4. log⁡12581=ln⁡81ln⁡125=4ln⁡33ln⁡5\log_{125}81 = \frac{\ln 81}{\ln 125} = \frac{4\ln 3}{3\ln 5}

Multiplying all factors:

5ln⁡23ln⁡3  ⋅  2ln⁡5ln⁡7  ⋅  ln⁡7ln⁡2  ⋅  4ln⁡33ln⁡5  =  5×2×43×3  ×  ln⁡2ln⁡2  ×  ln⁡3ln⁡3  ×  ln⁡5ln⁡5  ×  ln⁡7ln⁡7  =  409.\frac{5\ln 2}{3\ln 3} \;\cdot\; \frac{2\ln 5}{\ln 7} \;\cdot\; \frac{\ln 7}{\ln 2} \;\cdot\; \frac{4\ln 3}{3\ln 5} \;=\; \frac{5 \times 2 \times 4}{3 \times 3} \;\times\; \frac{\ln 2}{\ln 2} \;\times\; \frac{\ln 3}{\ln 3} \;\times\; \frac{\ln 5}{\ln 5} \;\times\; \frac{\ln 7}{\ln 7} \;=\; \frac{40}{9}.