Question

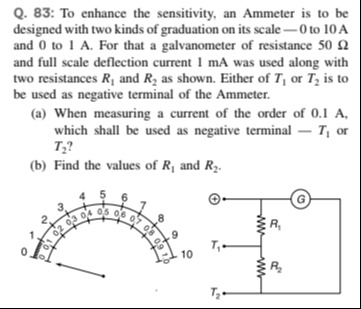
Q. 83: To enhance the sensitivity, an Ammeter is to be designed with two kinds of graduation on its scale - 0 to 10 A and 0 to 1 A. For that a galvanometer of resistance 50 $\Omega$ and full scale deflection current 1 mA was used along with two resistances $R_1$ and $R_2$ as shown. Either of $T_1$ or $T_2$ is to be used as negative terminal of the Ammeter.

(a) When measuring a current of the order of 0.1 A, which shall be used as negative terminal – $T_1$ or $T_2$?

(b) Find the values of $R_1$ and $R_2$.

Answer 1

(a) $T_2$

(b) $R_1 \approx 0.00500 \, \Omega$, $R_2 \approx 0.0450 \, \Omega$

Answer 2

The problem describes the design of a multi-range ammeter using a galvanometer and two resistances, $R_1$ and $R_2$. The ammeter has two ranges: 0 to 10 A and 0 to 1 A. We are given the galvanometer's resistance ($R_g$) and full-scale deflection current ($I_g$).

Given values:

Galvanometer resistance, $R_g = 50 \, \Omega$

Full-scale deflection current of galvanometer, $I_g = 1 \, \text{mA} = 1 \times 10^{-3} \, \text{A}$

Circuit Interpretation:

The diagram shows a common positive terminal ('+') and two selectable negative terminals ($T_1$ and $T_2$). This is a common configuration for a multi-range ammeter where the galvanometer is in parallel with a shunt resistance, and the shunt resistance changes depending on the selected range.

Let's analyze the shunt resistance for each range:

1. When $T_1$ is used as the negative terminal:
   The total current enters at '+' and exits at $T_1$.
   From the diagram, the galvanometer (G) is in parallel with the resistance $R_1$.
   So, the shunt resistance for this range is $R_{sh1} = R_1$.

2. When $T_2$ is used as the negative terminal:
   The total current enters at '+' and exits at $T_2$.
   From the diagram, the galvanometer (G) is in parallel with the series combination of $R_1$ and $R_2$.
   So, the shunt resistance for this range is $R_{sh2} = R_1 + R_2$.

Relating ranges to terminals:

For an ammeter, a smaller shunt resistance allows a larger current to be measured (higher range), as more current is bypassed from the galvanometer. Conversely, a larger shunt resistance allows a smaller current to be measured (lower range).

Since $R_1 < (R_1 + R_2)$, the shunt resistance $R_1$ corresponds to the higher current range, and the shunt resistance $(R_1 + R_2)$ corresponds to the lower current range.

Therefore:

• Using $T_1$ as the negative terminal corresponds to the 0 to 10 A range.
• Using $T_2$ as the negative terminal corresponds to the 0 to 1 A range.

(a) When measuring a current of the order of 0.1 A, which shall be used as negative terminal – $T_1$ or $T_2$?

A current of 0.1 A is best measured using the 0 to 1 A range for higher accuracy and sensitivity. As determined above, the 0 to 1 A range uses $T_2$ as the negative terminal.

(b) Find the values of $R_1$ and $R_2$.

The principle for an ammeter is that the voltage across the galvanometer and the shunt resistance is the same at full-scale deflection.

$I_g R_g = (I_{max} - I_g) R_{sh}$

Where $I_{max}$ is the full-scale current for the specific range.

For the 10 A range (using $T_1$):

$I_{max1} = 10 \, \text{A}$

$R_{sh1} = R_1$

$I_g R_g = (I_{max1} - I_g) R_1$

$(1 \times 10^{-3} \, \text{A}) \times (50 \, \Omega) = (10 \, \text{A} - 1 \times 10^{-3} \, \text{A}) R_1$

$0.05 = (9.999) R_1$

$R_1 = \frac{0.05}{9.999}$

$R_1 \approx 0.0050005 \, \Omega$

For the 1 A range (using $T_2$):

$I_{max2} = 1 \, \text{A}$

$R_{sh2} = R_1 + R_2$

$I_g R_g = (I_{max2} - I_g) (R_1 + R_2)$

$(1 \times 10^{-3} \, \text{A}) \times (50 \, \Omega) = (1 \, \text{A} - 1 \times 10^{-3} \, \text{A}) (R_1 + R_2)$

$0.05 = (0.999) (R_1 + R_2)$

$R_1 + R_2 = \frac{0.05}{0.999}$

$R_1 + R_2 \approx 0.05005005 \, \Omega$

Now, we can find $R_2$:

$R_2 = (R_1 + R_2) - R_1$

$R_2 = \frac{0.05}{0.999} - \frac{0.05}{9.999}$

$R_2 = 0.05 \left( \frac{1}{0.999} - \frac{1}{9.999} \right)$

$R_2 = 0.05 \left( \frac{9.999 - 0.999}{0.999 \times 9.999} \right)$

$R_2 = 0.05 \left( \frac{9}{9.989001} \right)$

$R_2 = \frac{0.45}{9.989001}$

$R_2 \approx 0.04504955 \, \Omega$

Rounding to a reasonable number of significant figures (e.g., 3-4):

$R_1 \approx 0.00500 \, \Omega$

$R_2 \approx 0.0450 \, \Omega$

(a) Answer:
For measuring a small current like 0.1 A, the 0-1 A range is more sensitive and accurate than the 0-10 A range. In this ammeter design, the 0-1 A range is achieved by using $T_2$ as the negative terminal, which places a larger shunt resistance ($R_1+R_2$) in parallel with the galvanometer, allowing less current to bypass the galvanometer for a given total current.

(b) Answer:
The values of $R_1$ and $R_2$ are calculated using the shunt formula $R_{sh} = \frac{I_g R_g}{I_{max} - I_g}$. For the 10 A range, the shunt is $R_1$. For the 1 A range, the shunt is $R_1+R_2$. Solving these two equations simultaneously yields the values for $R_1$ and $R_2$.