Question

If s-p mixing were not operative, then how many of the following would have different magnetism than it would with s-p mixing? $B_2, C_2, N_2, O_2, B_2^{2-}, B_2^{-}, C_2^{-}, N_2^{+}, O_2^{+}$

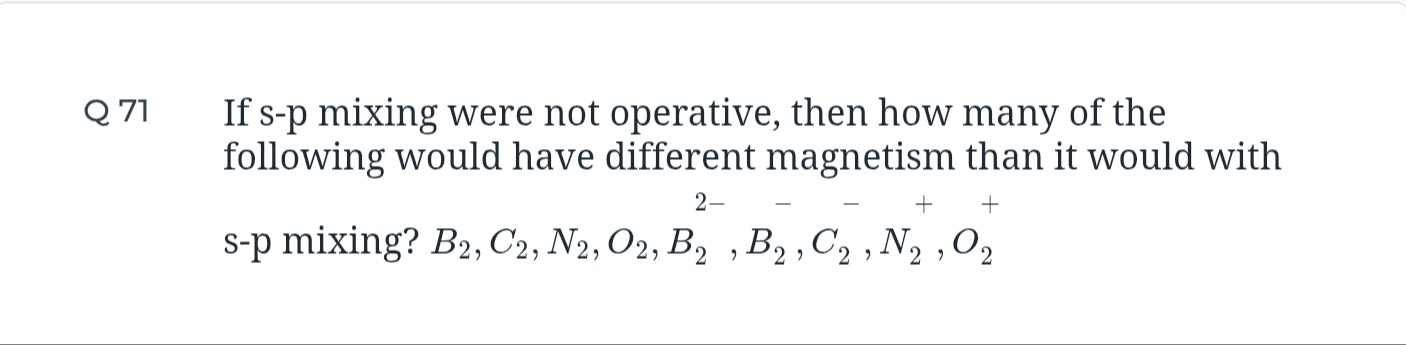
Answer 1

1

Answer 2

To determine how many of the given species would have different magnetism if s-p mixing were not operative, we need to compare their magnetic properties using two different molecular orbital (MO) energy level orders for diatomic molecules of second-period elements.

1. Understanding s-p mixing: For diatomic molecules of elements from Li$_2$ to N$_2$ (and their ions), the atomic orbitals $2s$ and $2p$ mix significantly. This mixing raises the energy of the $\sigma_{2p}$ orbital above the $\pi_{2p}$ orbitals.

• MO Order with s-p mixing: $\sigma_{2s} < \sigma^*_{2s} < \pi_{2p} < \sigma_{2p} < \pi^*_{2p} < \sigma^*_{2p}$

For diatomic molecules of O$_2$, F$_2$, and Ne$_2$ (and their ions), s-p mixing is not significant. The energy order is the standard one where $\sigma_{2p}$ is lower than $\pi_{2p}$.

• MO Order without significant s-p mixing: $\sigma_{2s} < \sigma^*_{2s} < \sigma_{2p} < \pi_{2p} < \pi^*_{2p} < \sigma^*_{2p}$

The question asks us to compare the magnetism in the scenario with s-p mixing (which is the actual MO diagram for B, C, N) versus the scenario without s-p mixing (which is a hypothetical diagram for B, C, N, but the actual diagram for O, F).

2. Analyzing each species: We will calculate the total number of valence electrons for each species and fill the MOs according to the two orders. A species is paramagnetic if it has unpaired electrons and diamagnetic if all electrons are paired.

The species are: $B_2, C_2, N_2, O_2, B_2^{2-}, B_2^{-}, C_2^{-}, N_2^{+}, O_2^{+}$.

Species with significant s-p mixing (B, C, N and their ions):

• MO Order (with s-p mixing): $\sigma_{2s} < \sigma^*_{2s} < \pi_{2p} < \sigma_{2p} < \pi^*_{2p} < \sigma^*_{2p}$
• MO Order (without s-p mixing): $\sigma_{2s} < \sigma^*_{2s} < \sigma_{2p} < \pi_{2p} < \pi^*_{2p} < \sigma^*_{2p}$

Species where s-p mixing is NOT significant (O and its ions):

• The MO order is the same in both scenarios: $\sigma_{2s} < \sigma^*_{2s} < \sigma_{2p} < \pi_{2p} < \pi^*_{2p} < \sigma^*_{2p}$. Therefore, $O_2$ and $O_2^{+}$ will not show a difference in magnetism.

Let's analyze the remaining species:

• $B_2$ (6 valence e⁻)

  • With s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \pi_{2p}^2. Unpaired e⁻: 2 ($\pi_{2p}$). Paramagnetic.
  • Without s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \sigma_{2p}^2. Unpaired e⁻: 0 ($\sigma_{2p}$). Diamagnetic.
  • Magnetism difference: YES

• $C_2$ (8 valence e⁻)

  • With s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \pi_{2p}^4. Unpaired e⁻: 0. Diamagnetic.
  • Without s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \sigma_{2p}^2 \pi_{2p}^2. Unpaired e⁻: 0. Diamagnetic.
  • Magnetism difference: NO

• $N_2$ (10 valence e⁻)

  • With s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \pi_{2p}^4 \sigma_{2p}^2. Unpaired e⁻: 0. Diamagnetic.
  • Without s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \sigma_{2p}^2 \pi_{2p}^4. Unpaired e⁻: 0. Diamagnetic.
  • Magnetism difference: NO

• $B_2^{2-}$ (6 + 2 = 8 valence e⁻)

  • With s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \pi_{2p}^4. Unpaired e⁻: 0. Diamagnetic.
  • Without s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \sigma_{2p}^2 \pi_{2p}^2. Unpaired e⁻: 0. Diamagnetic.
  • Magnetism difference: NO

• $B_2^{-}$ (6 + 1 = 7 valence e⁻)

  • With s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \pi_{2p}^3. Unpaired e⁻: 1 ($\pi_{2p}$). Paramagnetic.
  • Without s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \sigma_{2p}^1 \pi_{2p}^2. Unpaired e⁻: 1 ($\sigma_{2p}$). Paramagnetic.
  • Magnetism difference: NO

• $C_2^{-}$ (8 + 1 = 9 valence e⁻)

  • With s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \pi_{2p}^4 \sigma_{2p}^1. Unpaired e⁻: 1 ($\sigma_{2p}$). Paramagnetic.
  • Without s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \sigma_{2p}^2 \pi_{2p}^3. Unpaired e⁻: 1 ($\pi_{2p}$). Paramagnetic.
  • Magnetism difference: NO

• $N_2^{+}$ (10 - 1 = 9 valence e⁻)

  • With s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \pi_{2p}^4 \sigma_{2p}^1. Unpaired e⁻: 1 ($\sigma_{2p}$). Paramagnetic.
  • Without s-p mixing: \sigma_{2s}^2 \sigma^*_{2s}^2 \sigma_{2p}^1 \pi_{2p}^4. Unpaired e⁻: 1 ($\sigma_{2p}$). Paramagnetic.
  • Magnetism difference: NO

Only $B_2$ shows a change in magnetism (from paramagnetic to diamagnetic).

The species that exhibit a change in magnetism are those where the filling of $\pi_{2p}$ and $\sigma_{2p}$ orbitals differs in the two scenarios, leading to a different number of unpaired electrons. This occurs for $B_2$.

Summary of Magnetism:

Species	Valence e⁻	With s-p mixing	Without s-p mixing	Difference?
$B_2$	6	Paramagnetic	Diamagnetic	Yes
$C_2$	8	Diamagnetic	Diamagnetic	No
$N_2$	10	Diamagnetic	Diamagnetic	No
$O_2$	12	Paramagnetic	Paramagnetic	No
$B_2^{2-}$	8	Diamagnetic	Diamagnetic	No
$B_2^{-}$	7	Paramagnetic	Paramagnetic	No
$C_2^{-}$	9	Paramagnetic	Paramagnetic	No
$N_2^{+}$	9	Paramagnetic	Paramagnetic	No
$O_2^{+}$	11	Paramagnetic	Paramagnetic	No

Only one species, $B_2$, would have a different magnetism.

The final answer is $\boxed{1}$.