Question
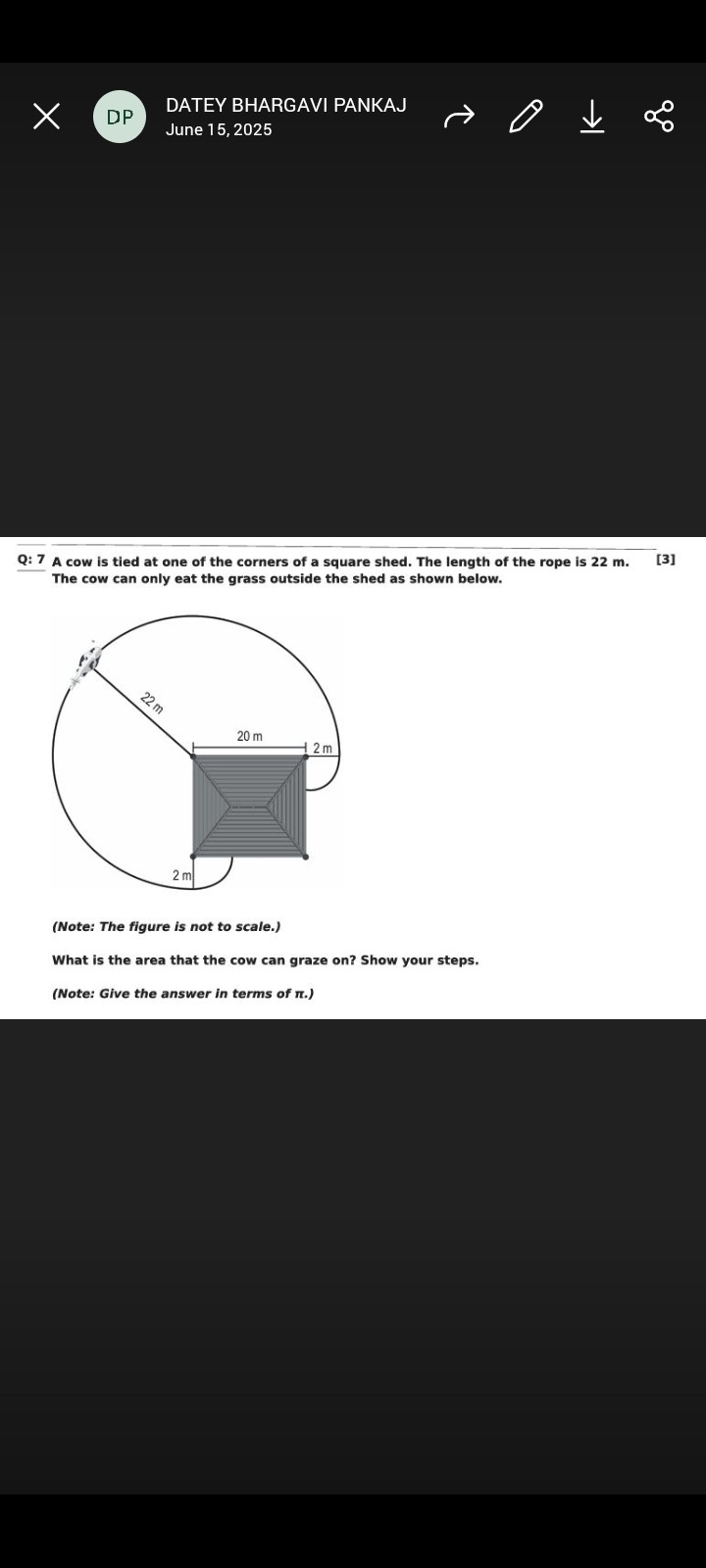
Question: A cow is tied at one of the corners of a square shed. The length of the rope is 22 m. The cow can o...
A cow is tied at one of the corners of a square shed. The length of the rope is 22 m.
The cow can only eat the grass outside the shed as shown below.
What is the area that the cow can graze on? Show your steps.
(Note: Give the answer in terms of π.)
The area that the cow can graze on is 365π m2.
Solution
The problem asks us to find the total area a cow can graze. The cow is tied at one corner of a square shed with a rope of length 22 m. The shed has a side length of 20 m. The cow can only eat grass outside the shed. The diagram shows that the rope can wrap around the adjacent corners of the shed.
We can break down the total grazing area into three parts:
-
The main grazing area: The cow is tied at one corner of the square shed. The area it can graze directly from this point, outside the shed, forms a large sector of a circle.
-
The radius of this sector is the length of the rope, R=22 m.
-
The angle of this sector is 360∘ minus the interior angle of the square (90∘), which is 270∘.
-
Area of the main sector (A1) = 360∘270∘×πR2
A1=43×π×(22)2
A1=43×π×484
A1=3×121π
A1=363π m2.
-
-
Grazing areas around the adjacent corners: When the rope extends along one side of the shed (length L=20 m), it reaches the next corner. The remaining length of the rope is R−L=22−20=2 m. This remaining length acts as the radius for a new sector formed around this adjacent corner.
-
The radius of each small sector is r=2 m.
-
Since it's a square corner, the angle of the turn (and thus the sector formed by the rope wrapping around) is 90∘.
-
Area of one small sector (A2) = 360∘90∘×πr2
A2=41×π×(2)2
A2=41×π×4
A2=π m2.
-
There are two such adjacent corners where the rope can wrap around, so the total area from these two sectors is 2×A2=2π m2.
-
-
Total grazing area: Sum the areas from the main sector and the two smaller sectors.
Total grazing area = A1+2×A2
Total grazing area = 363π+2π
Total grazing area = 365π m2.
The area that the cow can graze on is 365π m2.
