Question

If $a$ is the number of points of continuity of

$$f(x) = \begin{cases} x - 1, & \text{x is rational} \\ x^2 - x - 2, & \text{x is irrational} \end{cases}$$

b is the number of points of non-discontinuity of $f(x) = \text{sgn}(x^3 - 3x + 1), c$ is the number of points of non-differentiability of $f(x) = (\log x)|x^2 - 4x + 3| + 2(x - 2)^{1/3}$, and d is the number of points where the graph of $f(x) = (\log x)|x^2 - 4x + 3| + 2(x - 2)^{1/3}$ has a sharp turn then the value of $a + b + c + d$ is ____.

Answer 1

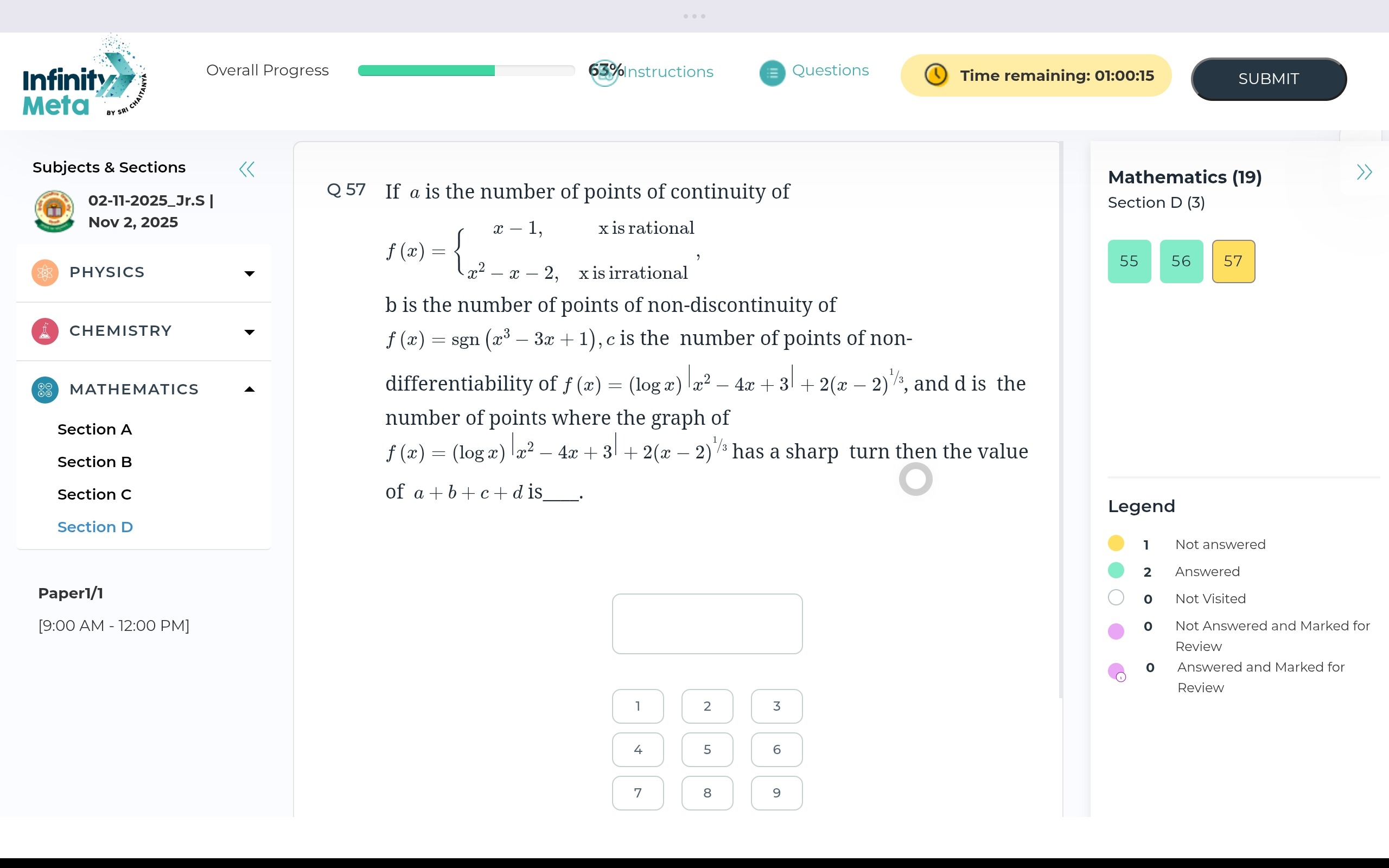
8

Answer 2

For $a$: Continuity occurs when $x-1 = x^2-x-2$, which gives $x^2-2x-1=0$. The roots are $x = 1 \pm \sqrt{2}$, which are irrational. Thus, there are 2 points of continuity. So, $a=2$.

For $b$: $\text{sgn}(x^3 - 3x + 1)$ is discontinuous when $x^3 - 3x + 1 = 0$. Let $g(x) = x^3 - 3x + 1$. $g'(x) = 3x^2 - 3$. Critical points are $x=\pm 1$. Local max at $x=-1$ is $g(-1)=3$. Local min at $x=1$ is $g(1)=-1$. Since the local max is positive and local min is negative, there are 3 real roots. Thus, $b=3$.

For $c$: $f(x) = (\log x)|x^2 - 4x + 3| + 2(x - 2)^{1/3}$. Domain is $x>0$. The term $|x^2 - 4x + 3|$ has points $x=1, 3$. The term $2(x - 2)^{1/3}$ is not differentiable at $x=2$. At $x=1$, $f'(1)=2/3$ (from both sides). Differentiable. At $x=3$, $f'_{-}(3) = 2/3 - 2 \log 3$ and $f'_{+}(3) = 2/3 + 2 \log 3$. Not differentiable. At $x=2$, the derivative of $2(x-2)^{1/3}$ is $\frac{2}{3(x-2)^{2/3}}$, which tends to $\infty$ as $x \to 2$. This is a point of non-differentiability (vertical tangent). Thus, $c=2$ (at $x=2$ and $x=3$).

For $d$: Sharp turns occur at points of continuity with finite but unequal left and right derivatives. At $x=3$, the derivatives are finite and unequal ($2/3 \mp 2 \log 3$). This is a sharp turn. At $x=2$, there is a vertical tangent, not a sharp turn. Thus, $d=1$ (at $x=3$).

$a+b+c+d = 2+3+2+1 = 8$.