Question

If $f(x) = \begin{cases} \frac{x\ln(\cos x)}{\ln(1+x^2)} \text{ for } x \neq 0 \\ 0 \text{ for } x=0, \end{cases}$ then

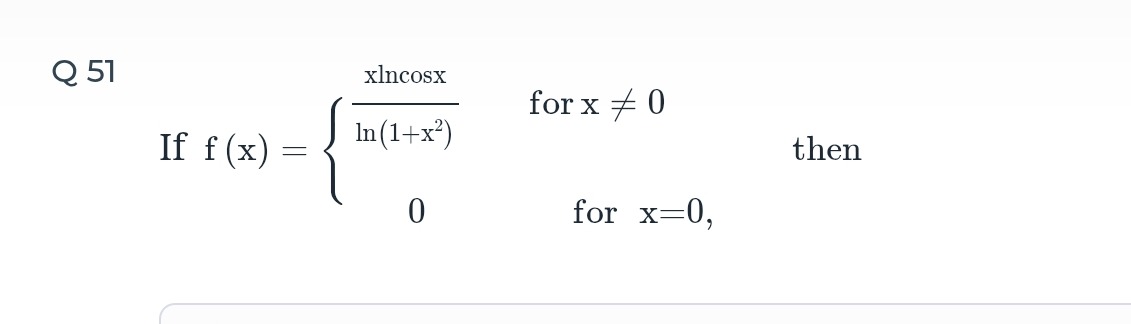
• A. f(x) is continuous at x=0
• B. f(x) is differentiable at x=0
• C. f'(0) = -1/2
• D. f(x) is continuous but not differentiable at x=0

Answer 1

Answer: (A), (B), (C)

f(x) is continuous at x=0, f(x) is differentiable at x=0, and f'(0) = -1/2.

Answer 2

To check for continuity at $x=0$, we evaluate $\lim_{x \to 0} f(x)$. Using Taylor series: $\ln(\cos x) \approx -\frac{x^2}{2}$ and $\ln(1+x^2) \approx x^2$. So, $\lim_{x \to 0} \frac{x(-\frac{x^2}{2})}{x^2} = \lim_{x \to 0} -\frac{x}{2} = 0$. Since $f(0)=0$, $f(x)$ is continuous at $x=0$.

To check for differentiability at $x=0$, we evaluate $f'(0) = \lim_{h \to 0} \frac{f(h)-f(0)}{h}$. $f'(0) = \lim_{h \to 0} \frac{1}{h} \left( \frac{h\ln(\cos h)}{\ln(1+h^2)} \right) = \lim_{h \to 0} \frac{\ln(\cos h)}{\ln(1+h^2)}$. Using Taylor series again: $\lim_{h \to 0} \frac{-\frac{h^2}{2}}{h^2} = -\frac{1}{2}$. Since the limit exists, $f(x)$ is differentiable at $x=0$ and $f'(0) = -1/2$.