Question
Question: If $f: R \rightarrow [-\frac{\pi}{4}, \frac{\pi}{2}], f(x) = \tan^{-1}(x^4 - x^2 -\frac{7}{4} + \tan...
If f:R→[−4π,2π],f(x)=tan−1(x4−x2−47+tan−1α) is a surjective function then which of the following is/are CORRECT?
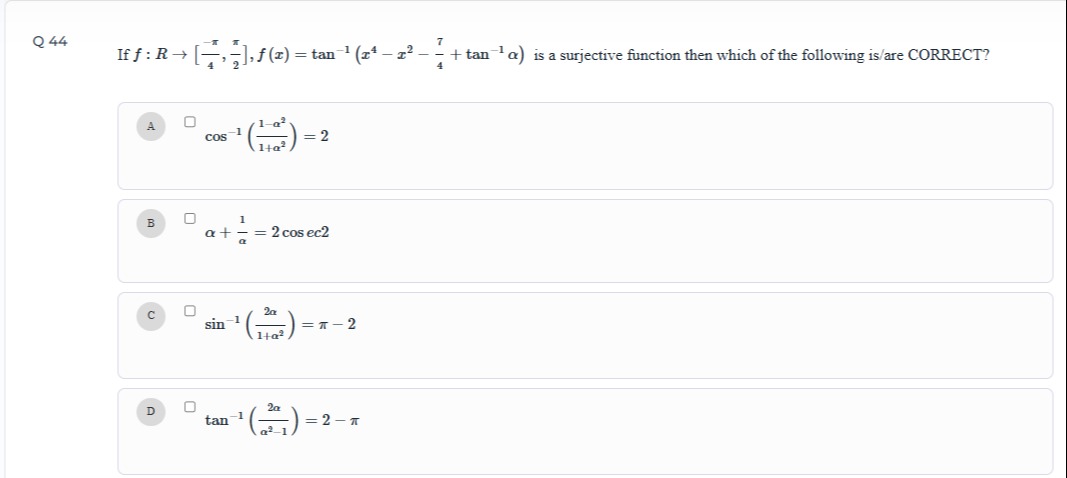
cos−1(1+α21−α2)=2
α+α1=2cosec2
sin−1(1+α22α)=π−2
tan−1(α2−12α)=2−π
A, B, C
Solution
The problem requires us to find the value of α for which the given function f(x) is surjective, and then check which of the provided options are correct.
The function is f:R→[−4π,2π], defined by f(x)=tan−1(x4−x2−47+tan−1α).
Step 1: Determine the range of the inner expression g(x)=x4−x2−47. Let t=x2. Since x∈R, t≥0. The expression becomes h(t)=t2−t−47. This is a quadratic function in t, representing a parabola opening upwards. Its vertex occurs at t=−2(1)(−1)=21. Since 21≥0, the minimum value of h(t) occurs at t=21. The minimum value is h(21)=(21)2−(21)−47=41−21−47=41−2−7=−48=−2. As t→∞ (which happens as x→∞ or x→−∞), h(t)→∞. Therefore, the range of g(x) is [−2,∞).
Step 2: Use the surjectivity condition to find tan−1α. Let C=tan−1α. The argument of the tan−1 function in f(x) is Y=g(x)+C. The range of Y is [−2+C,∞). The function f(x)=tan−1(Y). The standard range of tan−1(y) is (−2π,2π). For f(x) to be surjective onto the given codomain [−4π,2π]: The upper limit of the range of f(x) must be 2π. This is achieved as Y→∞, which is consistent with the range of Y being [−2+C,∞). The lower limit of the range of f(x) must be −4π. This occurs when Y takes its minimum value, Ymin=−2+C. So, we must have tan−1(Ymin)=−4π. tan−1(−2+C)=−4π −2+C=tan(−4π) −2+C=−1 C=1. Since C=tan−1α, we have tan−1α=1.
Step 3: Find the value of α. From tan−1α=1, we get α=tan(1). (Note: 1 is in radians).
Step 4: Check each option using α=tan(1). Let θ=1 radian. So α=tanθ.
-
Option A: cos−1(1+α21−α2) We know that 1+tan2θ1−tan2θ=cos(2θ). So, cos−1(1+tan2(1)1−tan2(1))=cos−1(cos(2)). Since 2 radians is approximately 2×57.3∘=114.6∘, which lies in the principal value range [0,π] for cos−1x. Therefore, cos−1(cos(2))=2. Option A is CORRECT.
-
Option B: α+α1 Substitute α=tan(1): tan(1)+tan(1)1=tan(1)+cot(1)=cos(1)sin(1)+sin(1)cos(1) =sin(1)cos(1)sin2(1)+cos2(1)=sin(1)cos(1)1. Multiply the numerator and denominator by 2: =2sin(1)cos(1)2=sin(2)2. We know that sin(2)1=csc(2) or cosec(2). So, α+α1=2csc(2). Option B is CORRECT.
-
Option C: sin−1(1+α22α) We know that 1+tan2θ2tanθ=sin(2θ). So, sin−1(1+tan2(1)2tan(1))=sin−1(sin(2)). Since 2 radians is approximately 114.6∘, it does not lie in the principal value range [−2π,2π] for sin−1x. We use the identity sinx=sin(π−x). So, sin−1(sin(2))=sin−1(sin(π−2)). Since π−2≈3.14159−2=1.14159 radians, which lies in [−2π,2π] (approximately [−1.57,1.57]). Therefore, sin−1(sin(2))=π−2. Option C is CORRECT.
-
Option D: tan−1(α2−12α) We know that 1−tan2θ2tanθ=tan(2θ). So, tan2θ−12tanθ=−1−tan2θ2tanθ=−tan(2θ). Substitute α=tan(1): tan−1(tan2(1)−12tan(1))=tan−1(−tan(2)). Using the property tan−1(−y)=−tan−1(y): =−tan−1(tan(2)). Since 2 radians is approximately 114.6∘, it does not lie in the principal value range (−2π,2π) for tan−1x. We use the identity tanx=tan(x−π). So, tan−1(tan(2))=tan−1(tan(2−π)). Since 2−π≈2−3.14159=−1.14159 radians, which lies in (−2π,2π) (approximately (−1.57,1.57)). Therefore, tan−1(tan(2))=2−π. So, tan−1(α2−12α)=−(2−π)=π−2. Option D states 2−π, which is incorrect.
