Question
Question: If $x_1, x_2$ and $x_3$ are the positive roots of the equation $x^3 - 6x^2 + 3px - 2p = 0, p \in R$ ...
If x1,x2 and x3 are the positive roots of the equation x3−6x2+3px−2p=0,p∈R then the value of sin−1(x11+x21)+cos−1(x21+x31)−tan−1(x31+x11) is greater than or equal to
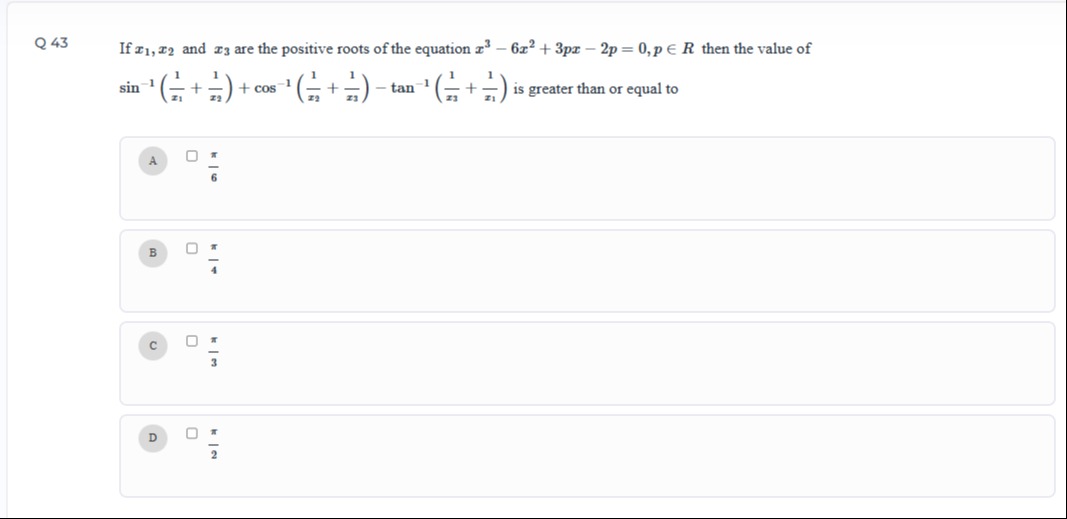
6π
4π
3π
2π
4π
Solution
The given cubic equation is x3−6x2+3px−2p=0. Let x1,x2,x3 be the positive roots of this equation.
From Vieta's formulas:
- x1+x2+x3=6
- x1x2+x2x3+x3x1=3p
- x1x2x3=2p
Since x1,x2,x3 are positive, x1x2x3=2p>0, thus, p>0.
Now, consider the sum of the reciprocals of the roots: x11+x21+x31=x1x2x3x2x3+x1x3+x1x2=2p3p=23.
Let y1=x11, y2=x21, y3=x31. Then y1,y2,y3 are positive, and y1+y2+y3=23.
The expression to evaluate is E=sin−1(x11+x21)+cos−1(x21+x31)−tan−1(x31+x11).
Using y1+y2+y3=23: E=sin−1(23−y3)+cos−1(23−y1)−tan−1(23−y2).
For the cubic equation to have three real roots, its discriminant must be non-negative. The discriminant Δ is given by: Δ=−108p3+864p2−1728p≥0. This simplifies to p(p−4)2≤0.
Since p>0 and (p−4)2≥0, the inequality can only hold if (p−4)2=0. This implies p=4.
Substitute p=4 into the original equation: x3−6x2+12x−8=0, which simplifies to (x−2)3=0. So, x1=x2=x3=2.
Since x1=x2=x3=2, we have y1=y2=y3=21.
Now substitute these values back into the expression for E: E=sin−1(21+21)+cos−1(21+21)−tan−1(21+21)=sin−1(1)+cos−1(1)−tan−1(1)=2π+0−4π=4π.
Thus, the value of the expression is 4π.
