Question
Question: The Image of the line $3x-y=2$ in the line $y=x-1$ is...
The Image of the line 3x−y=2 in the line y=x−1 is
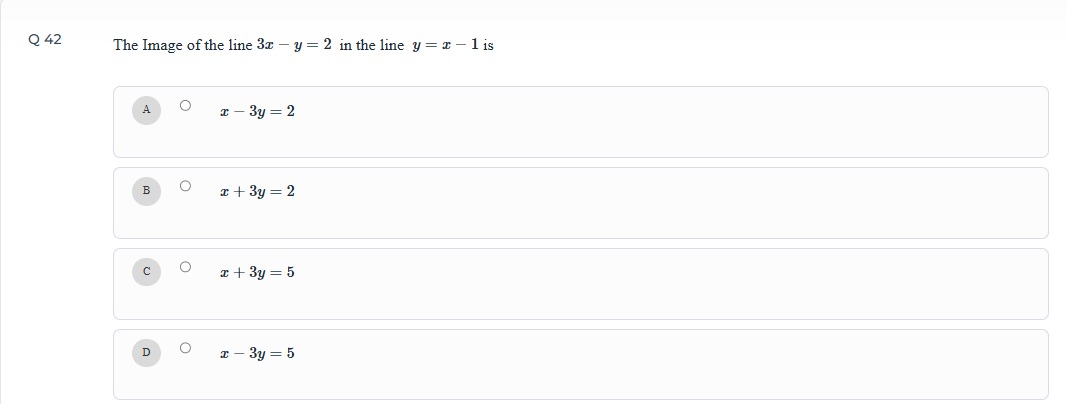
x−3y=2
x+3y=2
x+3y=5
x−3y=5
x - 3y = 2
Solution
To find the image of a line L1:3x−y=2 in the line Lm:y=x−1, we can follow these steps:
1. Find the point of intersection of the original line and the mirror line.
The intersection point P will lie on both the original line and its image. Given lines: L1:3x−y=2 Lm:y=x−1
Substitute y=x−1 from Lm into L1: 3x−(x−1)=2 3x−x+1=2 2x+1=2 2x=1 x=21
Now, find the corresponding y-coordinate using y=x−1: y=21−1=−21
So, the point of intersection is P(21,−21). This point must be on the image line.
2. Determine the slopes of the original line and the mirror line.
The equation of L1 is 3x−y=2, which can be rewritten as y=3x−2. The slope of L1 is m1=3.
The equation of Lm is y=x−1. The slope of Lm is mm=1.
3. Find the slope of the image line using the angle property.
Let Li be the image line and its slope be mi. The angle between the mirror line (Lm) and the original line (L1) is equal in magnitude but opposite in sign to the angle between the mirror line (Lm) and the image line (Li). The tangent of the angle θ1 from Lm to L1 is given by: tanθ1=1+m1mmm1−mm=1+(3)(1)3−1=42=21
The tangent of the angle θi from Lm to Li is given by: tanθi=1+mimmmi−mm
Since θi=−θ1, we have tanθi=−tanθ1. 1+mi(1)mi−1=−21 1+mimi−1=−21
Cross-multiply: 2(mi−1)=−(1+mi) 2mi−2=−1−mi 3mi=1 mi=31
4. Write the equation of the image line.
The image line passes through the point P(21,−21) and has a slope mi=31. Using the point-slope form y−y1=m(x−x1): y−(−21)=31(x−21) y+21=31x−61
To eliminate fractions, multiply the entire equation by the least common multiple of the denominators (which is 6): 6(y+21)=6(31x−61) 6y+3=2x−1
Rearrange the terms to the standard form Ax+By=C: 2x−6y=3+1 2x−6y=4
Divide the entire equation by 2: x−3y=2
This matches option A.
