Question

Let $f(x) = [\tan x [\cot x]], x \in [\frac{\pi}{12}, \frac{\pi}{4}]$ where $[x]$ denotes the greatest integer less than or equal to x. then which of the following is/are CORRECT?

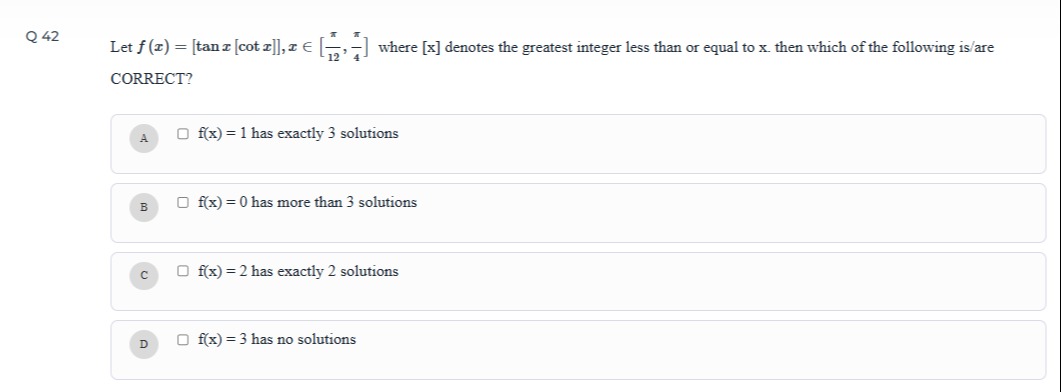
• A. $f(x) = 1$ has exactly 3 solutions
• B. $f(x) = 0$ has more than 3 solutions
• C. $f(x) = 2$ has exactly 2 solutions
• D. $f(x) = 3$ has no solutions

Answer 1

Answer: (A), (B), (D)

A, B, D

Answer 2

The function given is $f(x) = [\tan x [\cot x]]$ for $x \in [\frac{\pi}{12}, \frac{\pi}{4}]$. We need to analyze the values $f(x)$ takes in this interval.

First, let's determine the range of $\tan x$ and $\cot x$ in the given interval: For $x \in [\frac{\pi}{12}, \frac{\pi}{4}]$: $\tan x$ is an increasing function. $\tan(\frac{\pi}{12}) = \tan(15^\circ) = 2 - \sqrt{3} \approx 2 - 1.732 = 0.268$. $\tan(\frac{\pi}{4}) = \tan(45^\circ) = 1$. So, $\tan x \in [2-\sqrt{3}, 1]$.

$\cot x$ is a decreasing function. $\cot(\frac{\pi}{12}) = \cot(15^\circ) = 2 + \sqrt{3} \approx 2 + 1.732 = 3.732$. $\cot(\frac{\pi}{4}) = \cot(45^\circ) = 1$. So, $\cot x \in [1, 2+\sqrt{3}]$.

Now let's analyze the inner greatest integer function, $[\cot x]$: Since $\cot x \in [1, 2+\sqrt{3}]$, $[\cot x]$ can take integer values $1, 2, 3$.

We divide the interval $[\frac{\pi}{12}, \frac{\pi}{4}]$ into sub-intervals based on the value of $[\cot x]$. Let $x_1 = \cot^{-1}(3)$ and $x_2 = \cot^{-1}(2)$. Since $\cot x$ is decreasing, we have $\frac{\pi}{12} < x_1 < x_2 < \frac{\pi}{4}$. ($\cot(\frac{\pi}{12}) \approx 3.732$, $\cot(x_1)=3$, $\cot(x_2)=2$, $\cot(\frac{\pi}{4})=1$) This implies $\tan(x_1) = 1/3$ and $\tan(x_2) = 1/2$.

Case 1: $[\cot x] = 3$ This occurs when $3 \le \cot x < 4$. Since $\cot(\frac{\pi}{12}) = 2+\sqrt{3} \approx 3.732$, this condition is satisfied for $x \in [\frac{\pi}{12}, \cot^{-1}(3))$. So, for $x \in [\frac{\pi}{12}, x_1)$, $[\cot x] = 3$. In this interval, $f(x) = [\tan x \cdot 3]$. As $x$ goes from $\frac{\pi}{12}$ to $x_1$: $\tan x$ goes from $2-\sqrt{3}$ to $1/3$. So, $3 \tan x$ goes from $3(2-\sqrt{3}) \approx 3(0.268) = 0.804$ to $3(1/3) = 1$. Therefore, for $x \in [\frac{\pi}{12}, x_1)$, $3 \tan x \in [0.804, 1)$. Thus, $f(x) = [3 \tan x] = 0$ for $x \in [\frac{\pi}{12}, x_1)$. At $x = x_1 = \cot^{-1}(3)$, $\tan x_1 = 1/3$. So $f(x_1) = [3 \cdot \frac{1}{3}] = [1] = 1$.

Case 2: $[\cot x] = 2$ This occurs when $2 \le \cot x < 3$. This means $x \in (\cot^{-1}(3), \cot^{-1}(2))$. So, for $x \in (x_1, x_2)$, $[\cot x] = 2$. In this interval, $f(x) = [\tan x \cdot 2]$. As $x$ goes from $x_1$ to $x_2$: $\tan x$ goes from $1/3$ to $1/2$. So, $2 \tan x$ goes from $2(1/3) = 2/3 \approx 0.667$ to $2(1/2) = 1$. Therefore, for $x \in (x_1, x_2)$, $2 \tan x \in (2/3, 1)$. Thus, $f(x) = [2 \tan x] = 0$ for $x \in (x_1, x_2)$. At $x = x_2 = \cot^{-1}(2)$, $\tan x_2 = 1/2$. So $f(x_2) = [2 \cdot \frac{1}{2}] = [1] = 1$.

Case 3: $[\cot x] = 1$ This occurs when $1 \le \cot x < 2$. This means $x \in (\cot^{-1}(2), \cot^{-1}(1))$. We know $\cot^{-1}(1) = \frac{\pi}{4}$. So, for $x \in (x_2, \frac{\pi}{4})$, $[\cot x] = 1$. In this interval, $f(x) = [\tan x \cdot 1] = [\tan x]$. As $x$ goes from $x_2$ to $\frac{\pi}{4}$: $\tan x$ goes from $1/2$ to $1$. Therefore, for $x \in (x_2, \frac{\pi}{4})$, $\tan x \in (1/2, 1)$. Thus, $f(x) = [\tan x] = 0$ for $x \in (x_2, \frac{\pi}{4})$. At $x = \frac{\pi}{4}$, $\tan(\frac{\pi}{4}) = 1$. So $f(\frac{\pi}{4}) = [1] = 1$.

Summary of $f(x)$ values: $f(x) = 0$ for $x \in [\frac{\pi}{12}, x_1) \cup (x_1, x_2) \cup (x_2, \frac{\pi}{4})$. $f(x) = 1$ for $x \in \{x_1, x_2, \frac{\pi}{4}\}$.

Now let's evaluate the given options:

A. $f(x) = 1$ has exactly 3 solutions. From our analysis, $f(x) = 1$ at $x = \cot^{-1}(3)$, $x = \cot^{-1}(2)$, and $x = \frac{\pi}{4}$. These are three distinct solutions. Thus, option A is CORRECT.

B. $f(x) = 0$ has more than 3 solutions. $f(x) = 0$ for $x \in [\frac{\pi}{12}, x_1) \cup (x_1, x_2) \cup (x_2, \frac{\pi}{4})$. These are intervals, which contain infinitely many solutions. Thus, option B is CORRECT.

C. $f(x) = 2$ has exactly 2 solutions. Based on our analysis, $f(x)$ only takes values 0 and 1 in the given domain. It never takes the value 2. Thus, option C is INCORRECT.

D. $f(x) = 3$ has no solutions. Based on our analysis, $f(x)$ only takes values 0 and 1 in the given domain. It never takes the value 3. Thus, option D is CORRECT.

The correct options are A, B, and D.

Explanation of the solution: The function $f(x) = [\tan x [\cot x]]$ is analyzed over $x \in [\frac{\pi}{12}, \frac{\pi}{4}]$.

1. Determine the range of $\cot x$ and $[\cot x]$. $\cot x \in [1, 2+\sqrt{3}]$, so $[\cot x]$ can be $1, 2, 3$.
2. Divide the domain into sub-intervals based on the value of $[\cot x]$. Let $x_1 = \cot^{-1}(3)$ and $x_2 = \cot^{-1}(2)$.
   • For $x \in [\frac{\pi}{12}, x_1)$, $[\cot x] = 3$. $f(x) = [3 \tan x]$. Since $3 \tan x \in [3(2-\sqrt{3}), 1)$, $f(x)=0$.
   • At $x=x_1$, $f(x_1) = [3(1/3)] = 1$.
   • For $x \in (x_1, x_2)$, $[\cot x] = 2$. $f(x) = [2 \tan x]$. Since $2 \tan x \in (2/3, 1)$, $f(x)=0$.
   • At $x=x_2$, $f(x_2) = [2(1/2)] = 1$.
   • For $x \in (x_2, \frac{\pi}{4})$, $[\cot x] = 1$. $f(x) = [\tan x]$. Since $\tan x \in (1/2, 1)$, $f(x)=0$.
   • At $x=\frac{\pi}{4}$, $f(\frac{\pi}{4}) = [1] = 1$.
3. Summarize $f(x)$: $f(x)=1$ at $x_1, x_2, \frac{\pi}{4}$ (3 solutions). $f(x)=0$ over the intervals $[\frac{\pi}{12}, x_1)$, $(x_1, x_2)$, $(x_2, \frac{\pi}{4})$ (infinitely many solutions). $f(x)$ never takes values 2 or 3.
4. Evaluate options: A is correct, B is correct, C is incorrect, D is correct.