Question
Question: The equation of the plane containing two lines $\frac{x+1}{3}=\frac{y+3}{3}=\frac{z+5}{7}$ and $\fra...
The equation of the plane containing two lines 3x+1=3y+3=7z+5 and 1x−1=3y+3=λz+7 is (where λ∈R−{0})
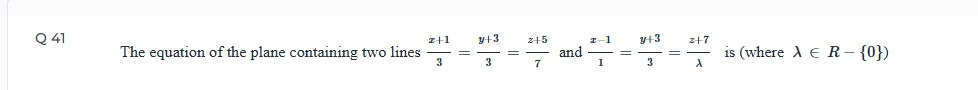
3x - 10y + 3z - 12 = 0
3x + 10y + 3z + 12 = 0
3x - 10y - 3z - 12 = 0
3x + 10y - 3z + 12 = 0
3x - 10y + 3z - 12 = 0
Solution
To find the equation of the plane containing two lines, we first identify a point on each line and their direction vectors.
For the first line, L1:3x+1=3y+3=7z+5, a point P1 is (−1,−3,−5) and its direction vector v1 is ⟨3,3,7⟩.
For the second line, L2:1x−1=3y+3=λz+7, a point P2 is (1,−3,−7) and its direction vector v2 is ⟨1,3,λ⟩.
For the plane to contain both lines, the lines must be coplanar. Since the direction vectors are not proportional, the lines must intersect. The condition for coplanarity is that the scalar triple product of the vector joining a point on each line and their direction vectors is zero: [P1P2,v1,v2]=0.
The vector P1P2=P2−P1=⟨1−(−1),−3−(−3),−7−(−5)⟩=⟨2,0,−2⟩.
Now, we compute the scalar triple product using a determinant: 231033−27λ=0 Expanding the determinant: 2(3λ−7×3)−0(3λ−7×1)+(−2)(3×3−3×1)=0 2(3λ−21)−0−2(9−3)=0 6λ−42−2(6)=0 6λ−42−12=0 6λ−54=0 6λ=54⟹λ=9. This value λ=9 satisfies the condition λ∈R−{0}.
Now, with λ=9, the direction vector for L2 is v2=⟨1,3,9⟩. The equation of the plane can be found using the determinant form with a point on the plane (e.g., P1) and the two direction vectors: x−x1a1a2y−y1b1b2z−z1c1c2=0 Using P1(−1,−3,−5), v1=⟨3,3,7⟩, and v2=⟨1,3,9⟩: x−(−1)31y−(−3)33z−(−5)79=0 x+131y+333z+579=0 Expanding this determinant: (x+1)(3×9−7×3)−(y+3)(3×9−7×1)+(z+5)(3×3−3×1)=0 (x+1)(27−21)−(y+3)(27−7)+(z+5)(9−3)=0 (x+1)(6)−(y+3)(20)+(z+5)(6)=0 Divide by 2: 3(x+1)−10(y+3)+3(z+5)=0 3x+3−10y−30+3z+15=0 3x−10y+3z−12=0.
