Question

If $y = Tan^{-1}(\frac{3+2\log_e x}{1-6\log_e x})+Tan^{-1}(\frac{\log_e(\frac{e}{x^2})}{\log_e(ex^2)})$, then $\frac{d^2y}{dx^2}$ is

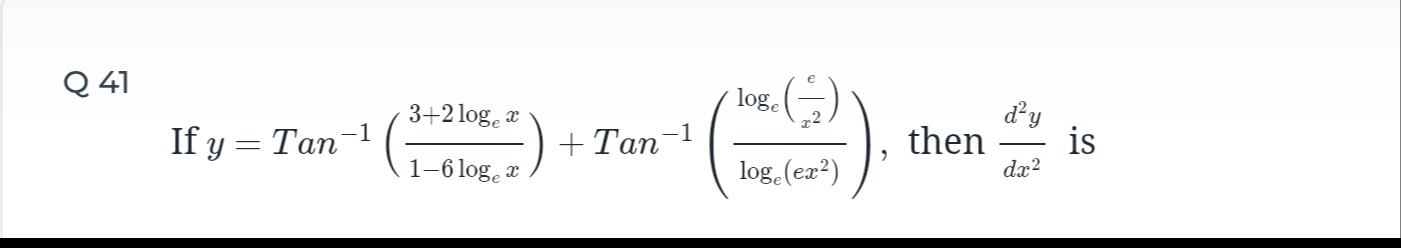
Answer 1

0

Answer 2

Let $u = \log_e x$. The function $y$ can be expressed as $y = Tan^{-1}\left(\frac{3+2u}{1-6u}\right)+Tan^{-1}\left(\frac{1-2u}{1+2u}\right)$. Differentiating $y$ with respect to $u$ yields $\frac{dy}{du} = \frac{2}{1+4u^2} - \frac{2}{1+4u^2} = 0$. Since $\frac{dy}{du}=0$, $y$ is a constant with respect to $u$, and thus a constant with respect to $x$. The first and second derivatives of a constant are zero.