Question

A point P(x, y) moves such that the sum of its distances from the lines $2x - y - 3 = 0$ and $x + 3y + 4 = 0$ is 7. The area bounded by the locus of P is

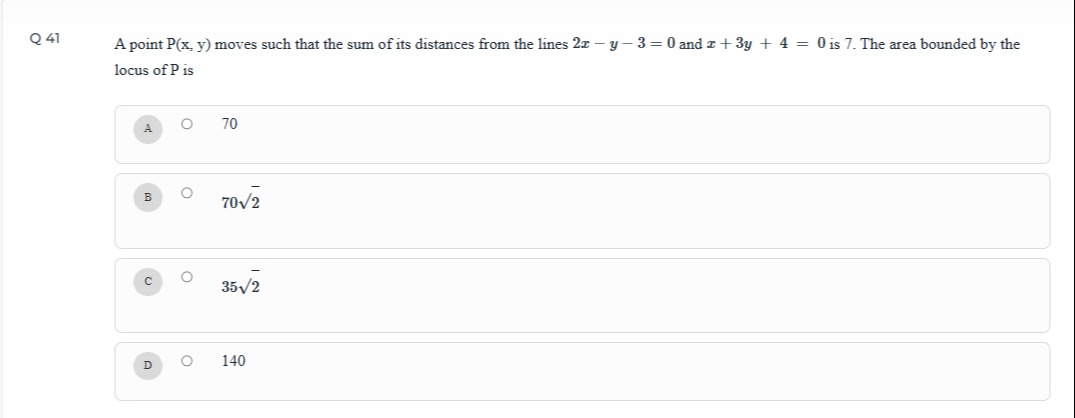
• A. 70
• B. $70\sqrt{2}$
• C. $35\sqrt{2}$
• D. 140

Answer 1

Answer: (B)

$70\sqrt{2}$

Answer 2

Let the two lines be $L_1: 2x - y - 3 = 0$ and $L_2: x + 3y + 4 = 0$. The distance of a point P(x, y) from a line $Ax + By + C = 0$ is given by the formula $d = \frac{|Ax + By + C|}{\sqrt{A^2 + B^2}}$.

The distance from $L_1$ is $d_1 = \frac{|2x - y - 3|}{\sqrt{2^2 + (-1)^2}} = \frac{|2x - y - 3|}{\sqrt{5}}$. The distance from $L_2$ is $d_2 = \frac{|x + 3y + 4|}{\sqrt{1^2 + 3^2}} = \frac{|x + 3y + 4|}{\sqrt{10}}$.

According to the problem, $d_1 + d_2 = 7$. So, the locus of P is given by the equation:

$$\frac{|2x - y - 3|}{\sqrt{5}} + \frac{|x + 3y + 4|}{\sqrt{10}} = 7$$

This type of equation, $|L_1'| + |L_2'| = K$, where $L_1'$ and $L_2'$ are normalized linear expressions (representing distances), describes a parallelogram.

To find the area of this parallelogram, we can use a change of variables. Let $U = \frac{2x - y - 3}{\sqrt{5}}$ and $V = \frac{x + 3y + 4}{\sqrt{10}}$. The equation of the locus in the UV-plane becomes $|U| + |V| = 7$.

The region described by $|U| + |V| = 7$ in the UV-plane is a square with vertices at $(7, 0)$, $(0, 7)$, $(-7, 0)$, and $(0, -7)$. The diagonals of this square lie along the U and V axes, and their length is $2 \times 7 = 14$. The area of a square with diagonal $d$ is $\frac{1}{2}d^2$. So, the area in the UV-plane is Area$_{UV} = \frac{1}{2}(14)^2 = \frac{1}{2}(196) = 98$ square units.

Now, we need to transform this area back to the xy-plane. The relationship between the areas is given by the Jacobian determinant of the transformation. The transformation from (x,y) to (U,V) is:

$U(x,y) = \frac{2}{\sqrt{5}}x - \frac{1}{\sqrt{5}}y - \frac{3}{\sqrt{5}}$

$V(x,y) = \frac{1}{\sqrt{10}}x + \frac{3}{\sqrt{10}}y + \frac{4}{\sqrt{10}}$

The Jacobian determinant of this transformation is:

$$J = \det \begin{pmatrix} \frac{\partial U}{\partial x} & \frac{\partial U}{\partial y} \\ \frac{\partial V}{\partial x} & \frac{\partial V}{\partial y} \end{pmatrix}$$ $$J = \det \begin{pmatrix} \frac{2}{\sqrt{5}} & \frac{-1}{\sqrt{5}} \\ \frac{1}{\sqrt{10}} & \frac{3}{\sqrt{10}} \end{pmatrix}$$ $$J = \left(\frac{2}{\sqrt{5}}\right)\left(\frac{3}{\sqrt{10}}\right) - \left(\frac{-1}{\sqrt{5}}\right)\left(\frac{1}{\sqrt{10}}\right)$$ $$J = \frac{6}{\sqrt{50}} + \frac{1}{\sqrt{50}} = \frac{7}{\sqrt{50}} = \frac{7}{5\sqrt{2}}$$

The area in the xy-plane is related to the area in the UV-plane by the formula: Area$_{xy} = \frac{\text{Area}_{UV}}{|J|}$

$$\text{Area}_{xy} = \frac{98}{\left|\frac{7}{5\sqrt{2}}\right|} = 98 \times \frac{5\sqrt{2}}{7}$$ $$\text{Area}_{xy} = (14 \times 7) \times \frac{5\sqrt{2}}{7} = 14 \times 5\sqrt{2} = 70\sqrt{2}$$

Thus, the area bounded by the locus of P is $70\sqrt{2}$.