Question

Absolute value of $\begin{vmatrix} 2a & 2b & b-c \\ 2b & 2a & a+c \\ a+b & a+b & b \end{vmatrix}$ is divisible by (where $a,b,c \in N$)

Answer 1

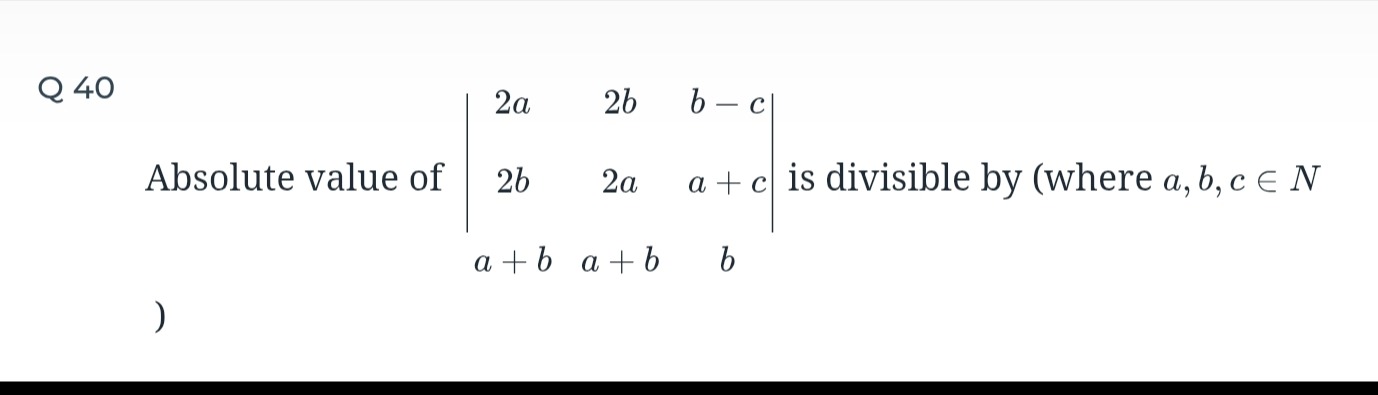
The absolute value of the determinant is $2(a+b)(a-b)^2$. This expression is divisible by $2$, $(a+b)$, $(a-b)$, and $(a-b)^2$.

Answer 2

The determinant $D$ is given by: $D = \begin{vmatrix} 2a & 2b & b-c \\ 2b & 2a & a+c \\ a+b & a+b & b \end{vmatrix}$

Apply $C_1 \to C_1 + C_2$: $D = \begin{vmatrix} 2a+2b & 2b & b-c \\ 2b+2a & 2a & a+c \\ a+b+a+b & a+b & b \end{vmatrix} = \begin{vmatrix} 2(a+b) & 2b & b-c \\ 2(a+b) & 2a & a+c \\ 2(a+b) & a+b & b \end{vmatrix}$

Take $2(a+b)$ common from $C_1$: $D = 2(a+b) \begin{vmatrix} 1 & 2b & b-c \\ 1 & 2a & a+c \\ 1 & a+b & b \end{vmatrix}$

Apply $R_2 \to R_2 - R_1$ and $R_3 \to R_3 - R_1$: $D = 2(a+b) \begin{vmatrix} 1 & 2b & b-c \\ 0 & 2a-2b & a+c-(b-c) \\ 0 & a+b-2b & b-(b-c) \end{vmatrix}$ $D = 2(a+b) \begin{vmatrix} 1 & 2b & b-c \\ 0 & 2(a-b) & a-b+2c \\ 0 & a-b & c \end{vmatrix}$

Expand along $C_1$: $D = 2(a+b) [1 \cdot (2(a-b)c - (a-b+2c)(a-b))]$ $D = 2(a+b) [2c(a-b) - (a-b)^2 - 2c(a-b)]$ $D = 2(a+b) [-(a-b)^2]$ $D = -2(a+b)(a-b)^2$

The absolute value is $|D| = |-2(a+b)(a-b)^2| = 2(a+b)(a-b)^2$ (since $a, b \in \mathbb{N}$, $a+b > 0$ and $(a-b)^2 \ge 0$). The expression $2(a+b)(a-b)^2$ is divisible by $2$, $(a+b)$, $(a-b)$, and $(a-b)^2$.