Question

$q,2q,3q\;$ and $4q\;$ charges at the four corners $A,B,C\;$ and $D$ of a square. The field at the centre $P$ of the square has the direction along

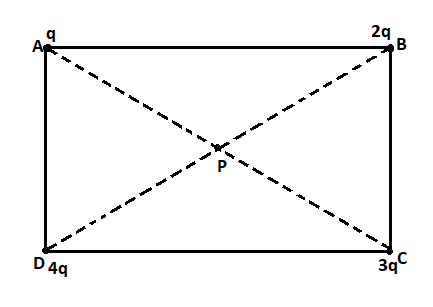
A. $AB\;$
B. $CB\;$
C. $AC\;$
D. $BD\;$

Answer 1

The space surrounding a charge where another charge can experience a force is known as the electric field. The intensity of the electrical field at any point is defined as the force experienced by a unit test charge placed at that point. Here we have to find the direction of the electric field at the point $P$ at the centre of the square.

Formula used: $E = \dfrac{{kQ}}{{{r^2}}}$
Where $E$ stands for the electric field at a particular point, $k = \dfrac{1}{{4\pi {\varepsilon _0}}}$ is a constant, $Q$ stands for the charge and $r$ stands for the distance between the charge and the point where we have to find the electric field.

Complete step by step answer:
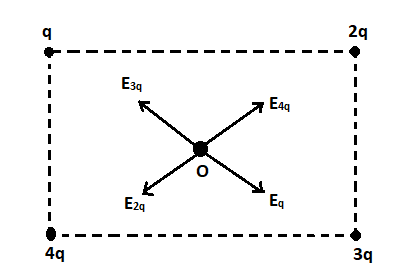
The direction of the electric field at the point $P$ due to the four charges is as shown in the figure below

The diagonal of the square can be obtained as shown below

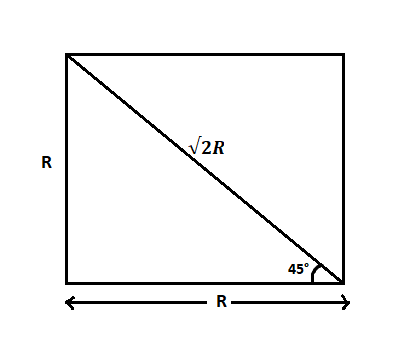
If $R$ is the length of the side of the square, then considering the right angled triangle as shown in the figure, the diagonal will be,
$d = \sqrt {{R^2} + {R^2}} = \sqrt {2{R^2}} = \sqrt 2 R$
The distance between each charge and the point $P$ will be the half of this diagonal.
That is,
$r = \dfrac{{\sqrt 2 R}}{2} = \dfrac{R}{{\sqrt 2 }}$
Now, we can write the electric fields as,
${E_{4q}} = \dfrac{{4kq}}{{{{\left( {\dfrac{R}{{\sqrt 2 }}} \right)}^2}}}$
For the charge $3q\;$ the electric field will be,
${E_{3q}} = \dfrac{{3kq}}{{{{\left( {\dfrac{R}{{\sqrt 2 }}} \right)}^2}}}$
The electric field for the charge $2q\;$ can be written as,
${E_{2q}} = \dfrac{{2kq}}{{{{\left( {\dfrac{R}{{\sqrt 2 }}} \right)}^2}}}$
The electric field for the charge $q$ can be written as,
${E_q} = \dfrac{{kq}}{{{{\left( {\dfrac{R}{{\sqrt 2 }}} \right)}^2}}}$
The resultant of this electric fields can be represented by the below diagram,

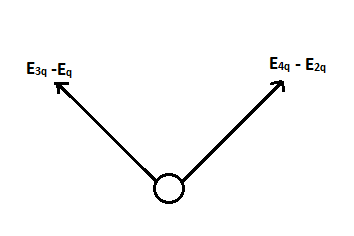
Now the resultant of ${E_{4q}} - {E_{2q}}$ can be written as,
${E_{4q}} - {E_{2q}} = \dfrac{{4kq}}{{{{\left( {\dfrac{R}{{\sqrt 2 }}} \right)}^2}}} - \dfrac{{2kq}}{{{{\left( {\dfrac{R}{{\sqrt 2 }}} \right)}^2}}}$
This can be written as,
${E_{4q}} - {E_{2q}} = \dfrac{{2kq}}{{\dfrac{{{R^2}}}{2}}} = \dfrac{{4kq}}{{{R^2}}}$
The resultant of ${E_{3q}} - {E_q}$ can be written as,
${E_{3q}} - {E_q} = \dfrac{{3kq}}{{{{\left( {\dfrac{R}{{\sqrt 2 }}} \right)}^2}}} - \dfrac{{kq}}{{{{\left( {\dfrac{R}{{\sqrt 2 }}} \right)}^2}}}$
This can be written as,
${E_{3q}} - {E_q} = \dfrac{{2kq}}{{\dfrac{{{R^2}}}{2}}} = \dfrac{{4kq}}{{{R^2}}}$
This can be represented as,

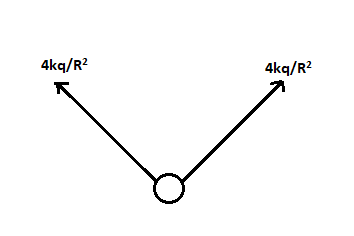
The resultant of these two vectors can be shown as,

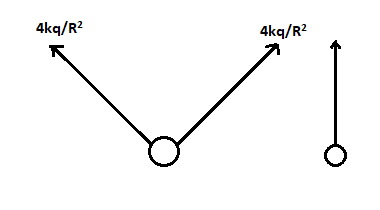
The magnitude of this resultant will be
${{E}_{res}}=2\times \frac{4kq\cos {{45}^{\circ }}}{{{R}^{2}}}=\frac{4\sqrt{2}kq}{{{R}^{2}}}$ $\left( \because \cos {{45}^{\circ }}=\frac{1}{\sqrt{2}} \right)$
The direction of the resultant electric field is along the direction of $CB\;$
Therefore, the correct answer is Option (B): $CB\;$

Note: The principle of superposition states that the resultant forces acting on a charge in a system of charges is the vector sum of the forces acting on the charge due to all other individual charges in the system. The direction of the force line gives the direction of the electric field.