Question

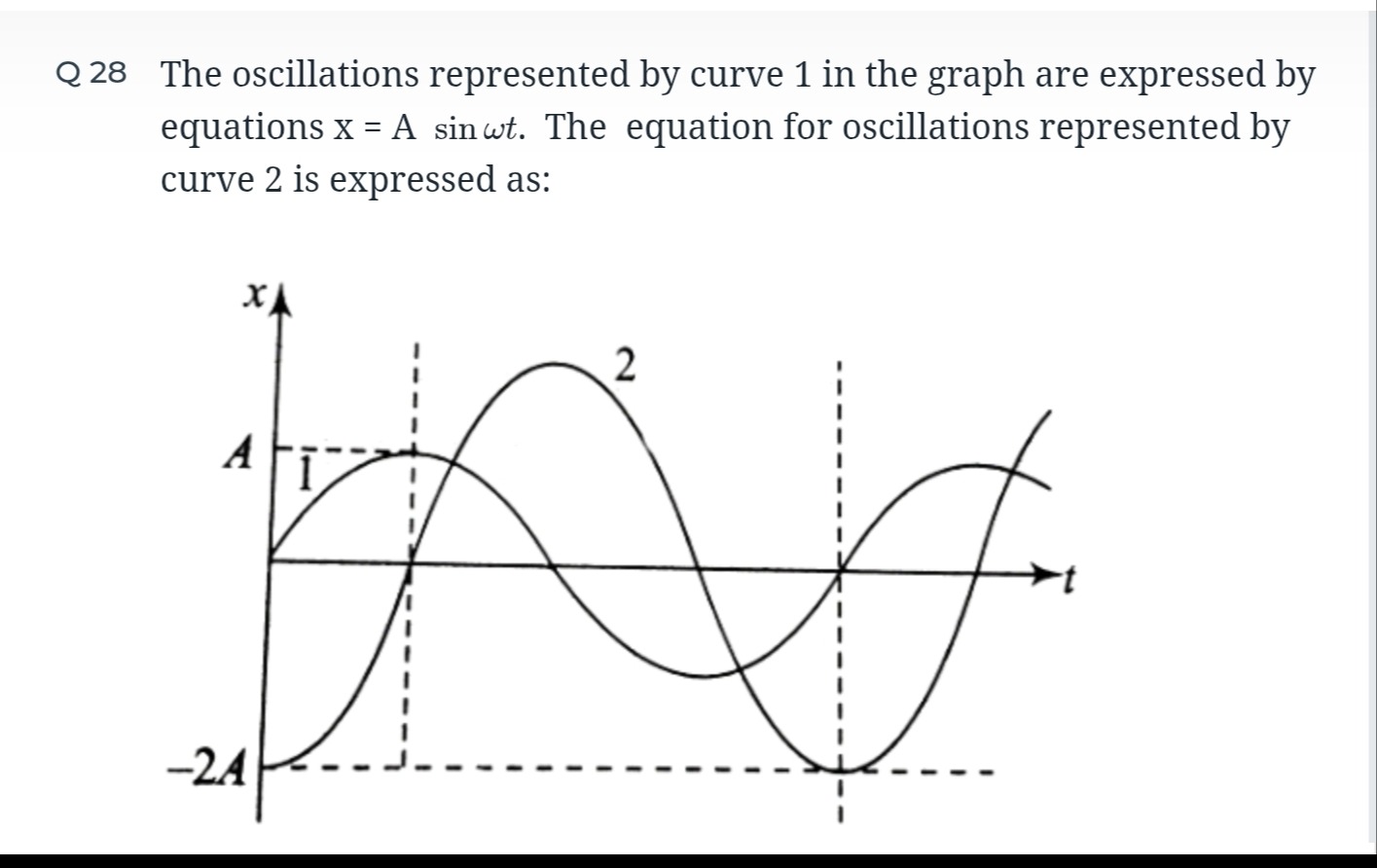
The oscillations represented by curve 1 in the graph are expressed by equations x = A sin⁡ωt. The equation for oscillations represented by curve 2 is expressed as:

Answer 1

x = -2A cos(ωt)

Answer 2

Curve 1 is a sine wave starting from 0 at t=0. Curve 2 has an amplitude of 2A and starts at x = -2A at t=0. Using the form $x_2(t) = A' \cos(\omega' t + \phi)$, with $A'=2A$ and $\omega'=\omega$, we have $x_2(t) = 2A \cos(\omega t + \phi)$. At t=0, $x_2(0) = -2A$, so $2A \cos(\phi) = -2A$, which means $\cos(\phi) = -1$. Thus, $\phi = \pi$. The equation becomes $x_2(t) = 2A \cos(\omega t + \pi) = -2A \cos(\omega t)$.