Question
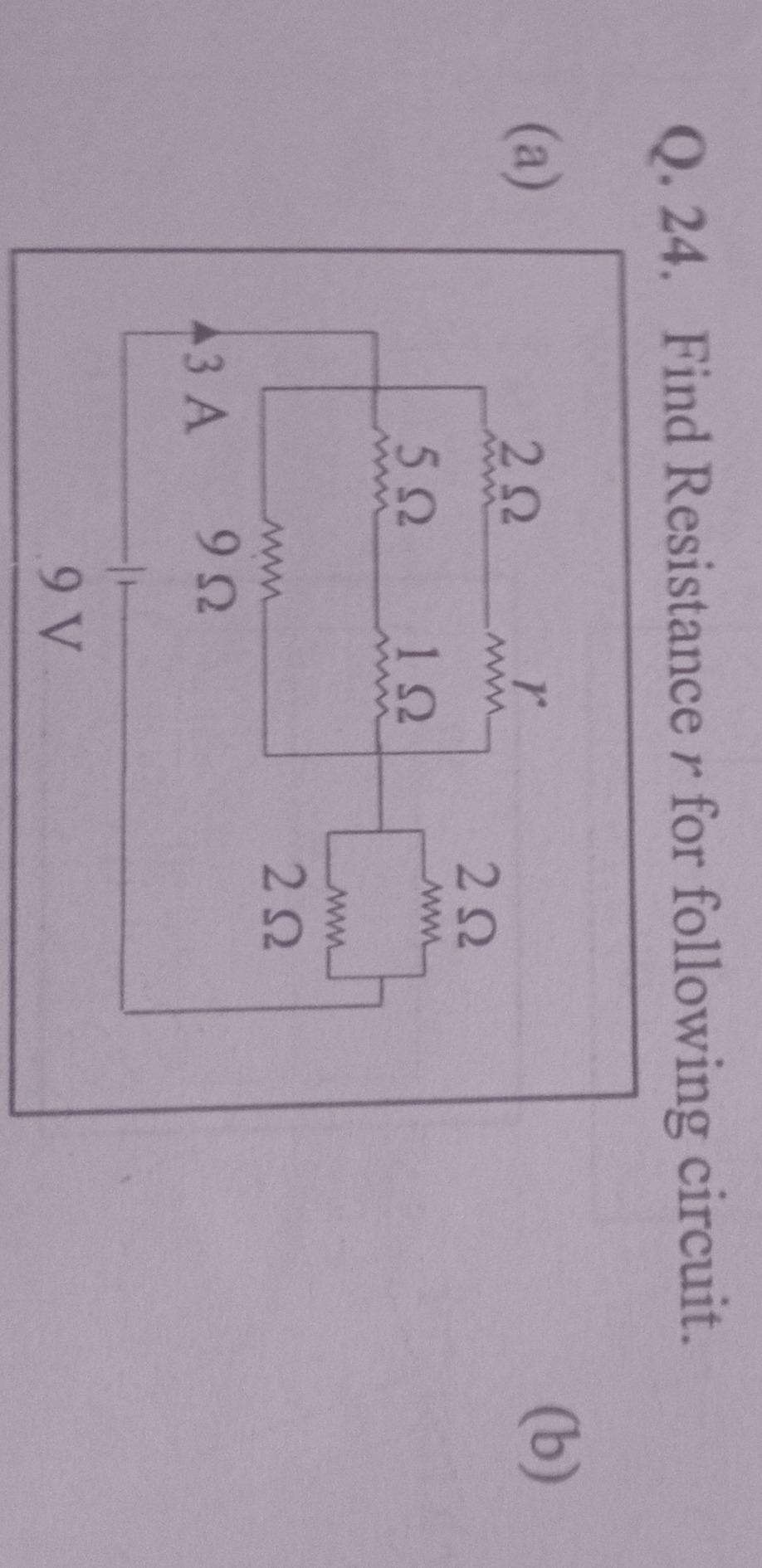
Question: Find Resistance r for following circuit. (a) A parallel circuit diagram is shown. A voltage source...
Find Resistance r for following circuit.
(a)
A parallel circuit diagram is shown. A voltage source of 9V is connected to a parallel combination of three branches. The first branch contains a 3A current source in parallel with a 9Ω resistor. The second branch contains a 5Ω resistor in series with a 2Ω resistor and an unknown resistance 'r'. The third branch contains two 2Ω resistors in series. All components are connected by wires. 2Ω r 2Ω 5Ω 1Ω 2Ω 43 A 9Ω 9V (b)
r = –359/53 Ω (approximately –6.77 Ω)
Solution
We can “find” the unknown resistance by “measuring” the effective resistance seen by the supply. In our (interpreted) circuit the 9‐V source is applied to three parallel branches:
-
In the first branch a 3 A current source is in parallel with a 9 Ω resistor. (It is best to first convert this Norton element to its Thevenin form. In fact a 3 A source in parallel with a 9 Ω resistor is equivalent to a 27 V source in series with 9 Ω. With a 9 V applied across it the branch current is I₁ = (27 – 9)/9 = 18/9 = 2 A.)
-
In the second branch a 5 Ω, a 2 Ω and an unknown resistor r are in series so that its resistance is R₂ = 5 + 2 + r = (7 + r) Ω.
-
In the third branch two 2 Ω resistors in series give R₃ = 2 + 2 = 4 Ω.
A known “measurement” in this circuit is that when looking into the network (that is, “turning off” the independent sources) the equivalent resistance is very low. (In fact the diagram tells us that if the 9 V source produces a current of 43 A then R_eq = 9/43 Ω.)
When “finding an equivalent resistance” using the standard procedure we turn off the independent sources. (A voltage source is replaced by a short circuit, and a current source by an open.) Hence the first branch becomes just the 9 Ω resistor. Then the three “resistances” are in parallel so that
1/R_eq = 1/9 + 1/(7 + r) + 1/4.
But we are told that R_eq = 9/43 Ω ⟹ 1/R_eq = 43/9.
Thus we have
43/9 = 1/9 + 1/(7 + r) + 1/4.
Let’s combine 1/9 and 1/4 first. Finding a common denominator: 1/9 + 1/4 = (4 + 9)/36 = 13/36.
So the equation becomes
43/9 = 13/36 + 1/(7 + r).
Now write 43/9 in terms of denominator 36: 43/9 = (43 × 4)/(9 × 4) = 172/36.
Thus
172/36 = 13/36 + 1/(7 + r) ⟹ 1/(7 + r) = (172 – 13)/36 = 159/36 = 53/12.
Taking reciprocals gives
7 + r = 12/53 ⟹ r = 12/53 – 7 = (12 – 7×53)/53 = (12 – 371)/53 = –359/53 Ω.
That is
r ≈ –6.77 Ω.
A negative value for r indicates that, to “balance” the network as shown the unknown element must supply power – i.e. it is a negative resistor (a device that may be synthesized using active elements).
