Question

The number of elements in the exhaustive set of values of x for which $f(x) = \sqrt[5]{x^2|x|^3} - \sqrt[3]{x^2|x|} - 1$ is not differentiable is

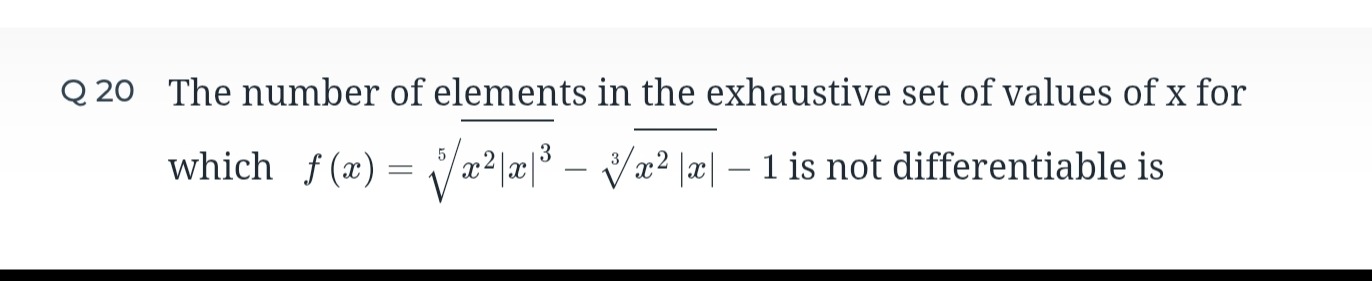
Answer 1

0

Answer 2

We simplify the function $f(x)$.

For the term $\sqrt[5]{x^2|x|^3}$: If $x \ge 0$, $\sqrt[5]{x^2 \cdot x^3} = \sqrt[5]{x^5} = x$. If $x < 0$, $\sqrt[5]{x^2 \cdot (-x)^3} = \sqrt[5]{x^2 \cdot (-x^3)} = \sqrt[5]{-x^5} = -x$. Thus, $\sqrt[5]{x^2|x|^3} = |x|$.

For the term $\sqrt[3]{x^2|x|}$: If $x \ge 0$, $\sqrt[3]{x^2 \cdot x} = \sqrt[3]{x^3} = x$. If $x < 0$, $\sqrt[3]{x^2 \cdot (-x)} = \sqrt[3]{-x^3} = -x$. Thus, $\sqrt[3]{x^2|x|} = |x|$.

Substituting these back into $f(x)$: $f(x) = |x| - |x| - 1 = -1$.

The function $f(x) = -1$ is a constant function, which is differentiable everywhere. Therefore, there are no points where $f(x)$ is not differentiable. The number of such points is 0.