Question

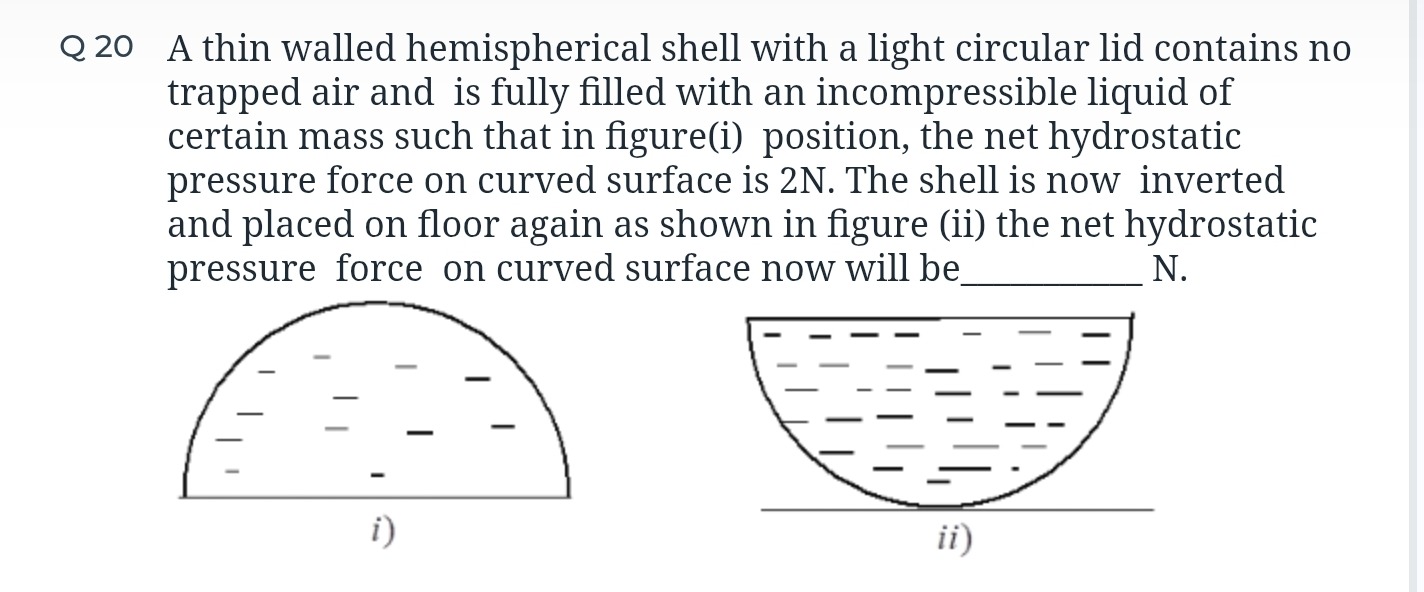
A thin walled hemispherical shell with a light circular lid contains no trapped air and is fully filled with an incompressible liquid of certain mass such that in figure(i) position, the net hydrostatic pressure force on curved surface is 2N. The shell is now inverted and placed on floor again as shown in figure (ii) the net hydrostatic pressure force on curved surface now will be ________ N.

Answer 1

2

Answer 2

Let $W$ be the weight of the incompressible liquid filling the hemispherical shell. Let $R$ be the radius of the hemisphere. Let $\rho$ be the density of the liquid and $g$ be the acceleration due to gravity. The volume of the liquid is $V = \frac{2}{3}\pi R^3$, so $W = \rho V g$.

In figure (i), the hemispherical shell is upright, with the curved surface at the bottom and the lid at the top. The net hydrostatic pressure force on the curved surface is given as $F_{curved,i} = 2N$. This force is exerted by the liquid on the curved surface. Due to symmetry, the horizontal component of this force is zero. The vertical component of the hydrostatic force exerted by the liquid on the curved surface is equal to the weight of the liquid column supported by this surface. In this configuration, the curved surface supports the entire weight of the liquid. Therefore, the upward vertical component of the force on the curved surface is equal to the weight of the liquid, $W$. Since the horizontal component is zero, the magnitude of the net hydrostatic pressure force on the curved surface is equal to its vertical component. Thus, $F_{curved,i} = W$. Given $F_{curved,i} = 2N$, we have $W = 2N$.

In figure (ii), the shell is inverted, with the curved surface at the top and the lid at the bottom, resting on the floor. The liquid fills the shell. We need to find the net hydrostatic pressure force on the curved surface, $F_{curved,ii}$. The liquid is contained by the curved surface and the lid. The forces acting on the liquid are its weight $W$ (downwards), the force exerted by the lid on the liquid (downwards), and the force exerted by the curved surface on the liquid (which is the reaction to $F_{curved,ii}$). Considering the vertical equilibrium of the liquid, the net upward force must balance the net downward force. The vertical component of the hydrostatic force exerted by the liquid on the curved surface is directed outwards from the liquid. In this inverted position, the curved surface is at the top. The liquid is below it. Therefore, the force on the curved surface is directed downwards. The magnitude of this downward vertical force is equal to the weight of the liquid column that would be above this surface if it were a free surface, or more generally, the weight of the liquid contained within the hemisphere. Thus, the downward vertical component of the force exerted by the liquid on the curved surface is $W$. Due to symmetry, the horizontal component of the force on the curved surface is zero. Therefore, the net hydrostatic pressure force on the curved surface in figure (ii) is a downward force of magnitude $W$. Since $W = 2N$, the net hydrostatic pressure force on the curved surface in figure (ii) is $2N$.