Question

For any values of a, b and c, $(a \square b) \diamond c = (a \diamond c) \square (b \diamond c)$.

Which of these operations could $\square$ and $\diamond$ respectively be?

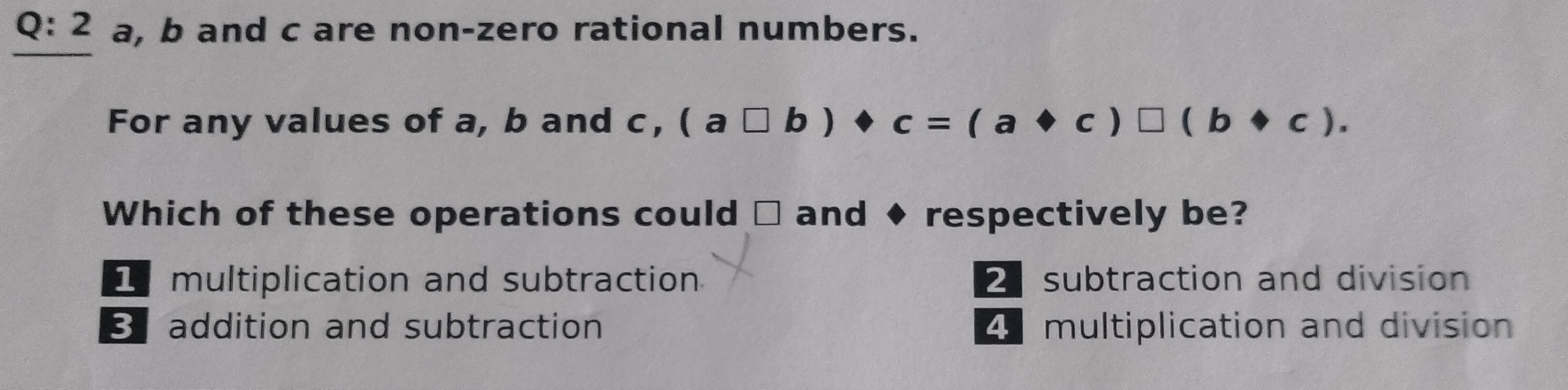
• A. multiplication and subtraction
• B. subtraction and division
• C. addition and subtraction
• D. multiplication and division

Answer 1

Answer: (B)

2

Answer 2

The given identity is $(a \square b) \diamond c = (a \diamond c) \square (b \diamond c)$. We need to find which pair of operations ($\square$, $\diamond$) satisfies this identity for any non-zero rational numbers a, b, and c.

Let's test each option:

Option 1: $\square$ is multiplication ($\times$), $\diamond$ is subtraction ($-$ ) LHS: $(a \times b) - c = ab - c$ RHS: $(a - c) \times (b - c) = ab - ac - bc + c^2$ For the identity to hold, $ab - c = ab - ac - bc + c^2$. This simplifies to $-c = -ac - bc + c^2$. Rearranging, we get $c^2 - ac - bc + c = 0$. Since c is a non-zero rational number, we can divide by c: $c - a - b + 1 = 0$ $c = a + b - 1$ This condition must hold for any values of a, b, c. However, $c = a + b - 1$ is a specific relationship between a, b, and c, not a universal truth. For example, if $a=1, b=1, c=2$, then $2 \neq 1+1-1$. So, this option is incorrect.

Option 2: $\square$ is subtraction ($-$ ), $\diamond$ is division ($\div$) LHS: $(a - b) \div c = \frac{a - b}{c}$ RHS: $(a \div c) - (b \div c) = \frac{a}{c} - \frac{b}{c} = \frac{a - b}{c}$ Here, LHS = RHS. This identity holds true for any non-zero rational numbers a, b, and c (since c is in the denominator, it must be non-zero, which is given). This is a standard property of division distributing over subtraction from the right. So, this option is correct.

Option 3: $\square$ is addition ($+$), $\diamond$ is subtraction ($-$ ) LHS: $(a + b) - c = a + b - c$ RHS: $(a - c) + (b - c) = a - c + b - c = a + b - 2c$ For the identity to hold, $a + b - c = a + b - 2c$. This simplifies to $-c = -2c$, which implies $c = 0$. However, c is given as a non-zero rational number. So, this option is incorrect.

Option 4: $\square$ is multiplication ($\times$), $\diamond$ is division ($\div$) LHS: $(a \times b) \div c = \frac{ab}{c}$ RHS: $(a \div c) \times (b \div c) = \frac{a}{c} \times \frac{b}{c} = \frac{ab}{c^2}$ For the identity to hold, $\frac{ab}{c} = \frac{ab}{c^2}$. Since a and b are non-zero, $ab \neq 0$. We can divide both sides by $ab$: $\frac{1}{c} = \frac{1}{c^2}$ This implies $c^2 = c$. Rearranging, $c^2 - c = 0$, so $c(c - 1) = 0$. Since c is a non-zero rational number, $c \neq 0$. Therefore, $c - 1 = 0$, which means $c = 1$. This condition must hold for any values of a, b, c. However, $c=1$ is a specific value for c, not a universal truth. So, this option is incorrect.

Based on the analysis, only Option 2 satisfies the given identity for any non-zero rational numbers a, b, and c.