Question

If $\overline{a}$ and $\overline{b}$ are non-Collinear vectors such that $|\overline{a}|= 2\sqrt{2}$, $|\overline{b}|= 3$ and angle between $\overline{a}$ & $\overline{b}$ is $\frac{\pi}{4}$. If $5\overline{a} + 2\overline{b}$ and $\overline{a} - 3\overline{b}$ are adjacent sides of a parallelogram then its area in square units is

Answer 1

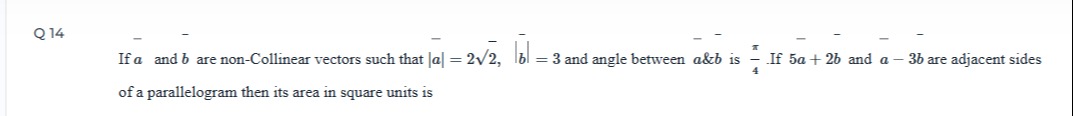
102

Answer 2

The area of a parallelogram with adjacent sides represented by vectors $\overline{u}$ and $\overline{v}$ is given by $|\overline{u} \times \overline{v}|$. Given adjacent sides are $\overline{u} = 5\overline{a} + 2\overline{b}$ and $\overline{v} = \overline{a} - 3\overline{b}$. The cross product is: $\overline{u} \times \overline{v} = (5\overline{a} + 2\overline{b}) \times (\overline{a} - 3\overline{b})$ Using the distributive property and properties of the cross product ($\overline{a} \times \overline{a} = \overline{0}$, $\overline{b} \times \overline{b} = \overline{0}$, $\overline{b} \times \overline{a} = -\overline{a} \times \overline{b}$): $\overline{u} \times \overline{v} = 5(\overline{a} \times \overline{a}) - 15(\overline{a} \times \overline{b}) + 2(\overline{b} \times \overline{a}) - 6(\overline{b} \times \overline{b})$ $\overline{u} \times \overline{v} = \overline{0} - 15(\overline{a} \times \overline{b}) + 2(-\overline{a} \times \overline{b}) - \overline{0}$ $\overline{u} \times \overline{v} = -17(\overline{a} \times \overline{b})$ The area of the parallelogram is the magnitude of this cross product: $\text{Area} = |\overline{u} \times \overline{v}| = |-17(\overline{a} \times \overline{b})| = 17 |\overline{a} \times \overline{b}|$ The magnitude of the cross product $|\overline{a} \times \overline{b}|$ is given by $|\overline{a}| |\overline{b}| \sin\theta$, where $\theta$ is the angle between $\overline{a}$ and $\overline{b}$. Given: $|\overline{a}| = 2\sqrt{2}$, $|\overline{b}| = 3$, and $\theta = \frac{\pi}{4}$. $|\overline{a} \times \overline{b}| = (2\sqrt{2})(3) \sin\left(\frac{\pi}{4}\right) = 6\sqrt{2} \left(\frac{1}{\sqrt{2}}\right) = 6$ Substituting this value back into the area formula: $\text{Area} = 17 \times 6 = 102$