Solveeit Logo
Login

Question

Question: $\lim_{x \to 0^+} ((x \cos x)^x + (x \sin x)^{1/x}) =$...

lim⁡x→0+((xcos⁡x)x+(xsin⁡x)1/x)=\lim_{x \to 0^+} ((x \cos x)^x + (x \sin x)^{1/x}) =

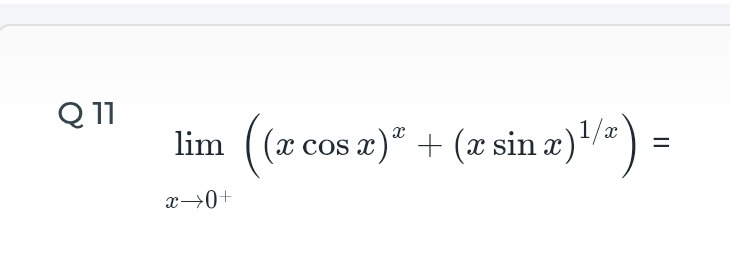
Answer

1

Explanation

Solution

The limit is evaluated by splitting it into two parts: L1=lim⁡x→0+(xcos⁡x)xL_1 = \lim_{x \to 0^+} (x \cos x)^x L2=lim⁡x→0+(xsin⁡x)1/xL_2 = \lim_{x \to 0^+} (x \sin x)^{1/x} For L1L_1, let y=(xcos⁡x)xy = (x \cos x)^x. Then ln⁡y=xln⁡(xcos⁡x)=xln⁡x+xln⁡(cos⁡x)\ln y = x \ln(x \cos x) = x \ln x + x \ln(\cos x). Using L'Hopital's rule for lim⁡x→0+xln⁡x=lim⁡x→0+ln⁡x1/x=lim⁡x→0+1/x−1/x2=0\lim_{x \to 0^+} x \ln x = \lim_{x \to 0^+} \frac{\ln x}{1/x} = \lim_{x \to 0^+} \frac{1/x}{-1/x^2} = 0. Also, lim⁡x→0+xln⁡(cos⁡x)=0⋅ln⁡(1)=0\lim_{x \to 0^+} x \ln(\cos x) = 0 \cdot \ln(1) = 0. So, lim⁡x→0+ln⁡y=0\lim_{x \to 0^+} \ln y = 0, which means L1=e0=1L_1 = e^0 = 1.

For L2L_2, let z=(xsin⁡x)1/xz = (x \sin x)^{1/x}. Then ln⁡z=1xln⁡(xsin⁡x)=ln⁡x+ln⁡(sin⁡x)x\ln z = \frac{1}{x} \ln(x \sin x) = \frac{\ln x + \ln(\sin x)}{x}. As x→0+x \to 0^+, the numerator ln⁡x+ln⁡(sin⁡x)→−∞\ln x + \ln(\sin x) \to -\infty and the denominator x→0+x \to 0^+. Thus, lim⁡x→0+ln⁡z=−∞\lim_{x \to 0^+} \ln z = -\infty, which means L2=e−∞=0L_2 = e^{-\infty} = 0.

The total limit is L1+L2=1+0=1L_1 + L_2 = 1 + 0 = 1.