Question

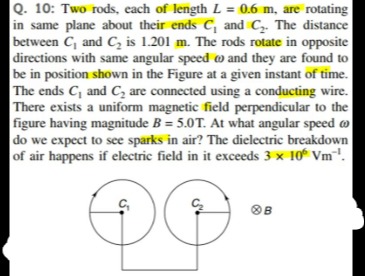
Two rods, each of length L = 0.6 m, are rotating in same plane about their ends $C_1$ and $C_2$. The distance between $C_1$ and $C_2$ is 1.201 m. The rods rotate in opposite directions with same angular speed $\omega$ and they are found to be in position shown in the Figure at a given instant of time. The ends $C_1$ and $C_2$ are connected using a conducting wire. There exists a uniform magnetic field perpendicular to the figure having magnitude B = 5.0T. At what angular speed $\omega$ do we expect to see sparks in air? The dielectric breakdown of air happens if electric field in it exceeds $3 \times 10^6 Vm^{-1}$.

Answer 1

1667 rad/s

Answer 2

The problem describes two rotating rods in a uniform magnetic field, with their pivots connected by a conducting wire. We need to find the angular speed at which the electric field in the air gap between the free ends of the rods exceeds the dielectric breakdown strength of air, causing sparks.

1. Induced EMF in a Rotating Rod: Consider a rod of length L rotating with angular speed $\omega$ about one of its ends in a uniform magnetic field B perpendicular to the plane of rotation. The motional EMF induced across the rod is given by: $EMF = \frac{1}{2} B\omega L^2$

2. Potential Difference Between the Free Ends: Let $C_1$ and $C_2$ be the pivots and $P_1$ and $P_2$ be the free ends of the rods. The magnetic field B is directed into the page ($\otimes$). The left rod (pivot $C_1$) rotates counter-clockwise (CCW). Using the right-hand rule for $\vec{v} \times \vec{B}$, the force on positive charges is directed outwards along the rod. Therefore, $P_1$ is at a higher potential than $C_1$. $V_{P_1} - V_{C_1} = \frac{1}{2} B\omega L^2$

The right rod (pivot $C_2$) rotates clockwise (CW). Using the right-hand rule for $\vec{v} \times \vec{B}$, the force on positive charges is directed inwards towards $C_2$. Therefore, $C_2$ is at a higher potential than $P_2$. $V_{C_2} - V_{P_2} = \frac{1}{2} B\omega L^2$

Since the ends $C_1$ and $C_2$ are connected by a conducting wire, their potentials are equal: $V_{C_1} = V_{C_2}$. Let's set this common potential to $V_0$. So, $V_{P_1} = V_0 + \frac{1}{2} B\omega L^2$. And $V_{P_2} = V_0 - \frac{1}{2} B\omega L^2$.

The potential difference between the free ends $P_1$ and $P_2$ is: $\Delta V = V_{P_1} - V_{P_2} = \left(V_0 + \frac{1}{2} B\omega L^2\right) - \left(V_0 - \frac{1}{2} B\omega L^2\right)$ $\Delta V = B\omega L^2$

3. Distance Between the Free Ends: The length of each rod is $L = 0.6$ m. The distance between the pivots $C_1$ and $C_2$ is $D = 1.201$ m. When the rods are in the horizontal position shown, the distance between their free ends $P_1$ and $P_2$ is: $d = D - L - L = D - 2L$ $d = 1.201 \text{ m} - 2 \times 0.6 \text{ m} = 1.201 \text{ m} - 1.2 \text{ m} = 0.001 \text{ m}$

4. Electric Field in the Air Gap: The electric field in the air gap between $P_1$ and $P_2$ is: $E = \frac{\Delta V}{d} = \frac{B\omega L^2}{D - 2L}$

5. Condition for Sparks: Sparks occur when the electric field $E$ exceeds the dielectric breakdown strength of air, $E_{breakdown} = 3 \times 10^6 \text{ Vm}^{-1}$. So, we need $E \ge E_{breakdown}$: $\frac{B\omega L^2}{D - 2L} \ge E_{breakdown}$

Solving for $\omega$: $\omega \ge \frac{E_{breakdown} (D - 2L)}{B L^2}$

6. Calculation: Substitute the given values: $E_{breakdown} = 3 \times 10^6 \text{ Vm}^{-1}$ $D - 2L = 0.001 \text{ m}$ $B = 5.0 \text{ T}$ $L = 0.6 \text{ m}$, so $L^2 = (0.6)^2 = 0.36 \text{ m}^2$

$\omega \ge \frac{(3 \times 10^6 \text{ Vm}^{-1}) \times (0.001 \text{ m})}{(5.0 \text{ T}) \times (0.36 \text{ m}^2)}$ $\omega \ge \frac{3 \times 10^3}{1.8}$ $\omega \ge \frac{3000}{1.8}$ $\omega \ge \frac{30000}{18}$ $\omega \ge \frac{5000}{3} \text{ rad/s}$ $\omega \ge 1666.67 \text{ rad/s}$

The minimum angular speed at which sparks are expected to be seen is approximately 1667 rad/s.

Explanation of the solution:

1. Calculate the induced EMF across each rotating rod using $EMF = \frac{1}{2} B\omega L^2$.
2. Determine the potential difference between the free ends of the rods. Due to opposite rotation and common pivot connection, the potential difference is $B\omega L^2$.
3. Calculate the physical gap distance between the free ends: $d = D - 2L$.
4. Calculate the electric field in the gap using $E = \frac{\Delta V}{d}$.
5. Set the calculated electric field equal to the dielectric breakdown strength of air ($E_{breakdown} = 3 \times 10^6 \text{ Vm}^{-1}$) to find the minimum angular speed $\omega$.
6. Substitute the given values to get $\omega = \frac{E_{breakdown} (D - 2L)}{B L^2} = \frac{(3 \times 10^6)(0.001)}{(5.0)(0.36)} = \frac{5000}{3} \approx 1667 \text{ rad/s}$.