Question

Let $f(x) = x^2 \cos x - 2x \sin x - 2 \cos x$, $g(x) = x^3 + x^2 \sin x + 2x \cos x - 2 \sin x$.

Let $L_2 = \lim_{x \to \infty} \frac{f'(x)}{g'(x)}$, $L_1 = \lim_{x \to \infty} \frac{f(x)}{g(x)}$. Then select incorrect alternative/s.

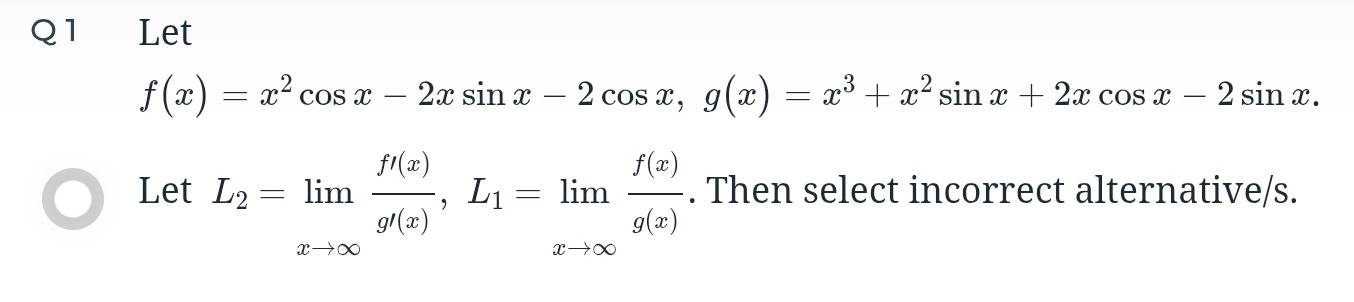
• A. $L_1 = 0$
• B. $L_2$ does not exist
• C. $L_1 = L_2$
• D. $L_1 = 1/3$

Answer 1

Answer: (A), (B)

L1 = L2, L1 = 1/3

Answer 2

We first find the derivatives of $f(x)$ and $g(x)$: $f'(x) = \frac{d}{dx}(x^2 \cos x - 2x \sin x - 2 \cos x) = (2x \cos x - x^2 \sin x) - (2 \sin x + 2x \cos x) - (-2 \sin x) = -x^2 \sin x$. $g'(x) = \frac{d}{dx}(x^3 + x^2 \sin x + 2x \cos x - 2 \sin x) = 3x^2 + (2x \sin x + x^2 \cos x) + (2 \cos x - 2x \sin x) - (2 \cos x) = 3x^2 + x^2 \cos x = x^2(3 + \cos x)$.

Now, we compute $L_2$: $L_2 = \lim_{x \to \infty} \frac{f'(x)}{g'(x)} = \lim_{x \to \infty} \frac{-x^2 \sin x}{x^2(3 + \cos x)} = \lim_{x \to \infty} \frac{-\sin x}{3 + \cos x}$. Since $\sin x$ and $\cos x$ oscillate between -1 and 1, and $3 + \cos x$ is always between 2 and 4, the limit $L_2$ does not exist.

Next, we compute $L_1$: $L_1 = \lim_{x \to \infty} \frac{f(x)}{g(x)} = \lim_{x \to \infty} \frac{x^2 \cos x - 2x \sin x - 2 \cos x}{x^3 + x^2 \sin x + 2x \cos x - 2 \sin x}$. Divide numerator and denominator by $x^3$: $L_1 = \lim_{x \to \infty} \frac{\frac{\cos x}{x} - \frac{2 \sin x}{x^2} - \frac{2 \cos x}{x^3}}{1 + \frac{\sin x}{x} + \frac{2 \cos x}{x^2} - \frac{2 \sin x}{x^3}}$. As $x \to \infty$, all terms with $x$ in the denominator go to 0. $L_1 = \frac{0 - 0 - 0}{1 + 0 + 0 - 0} = 0$.

So, $L_1 = 0$ and $L_2$ does not exist. The incorrect alternatives are those stating that $L_1 = L_2$ (since $L_2$ does not exist and $L_1=0$) and $L_1 = 1/3$ (since $L_1=0$).