Question

Pulleys and strings are massless. The horizontal surface is smooth. The acceleration of the block A is

$A){\text{ }}\dfrac{F}{{2M}}$
$B){\text{ }}\dfrac{F}{M}$
$C){\text{ }}\dfrac{{2F}}{M}$
$D){\text{ }}\dfrac{M}{{2F}}$

Answer 1

In order to solve the question, we will first of all make the free body diagram of whole system then we will use the net force formula on free body diagram of pulley to find tension and then we will use net force formula on free body diagram of block – A along with this the tension we found to find the acceleration.

Formula Used:
${F_{Net}} = ma$
${F_{Net}}$ refers to net force applied
M refers to mass
a refers to acceleration

Complete step by step solution:
In the question we are given a body of mass M tied to pulley which is connected to another pulley and that pulley is tied on the ceiling and we have to find the acceleration of block A

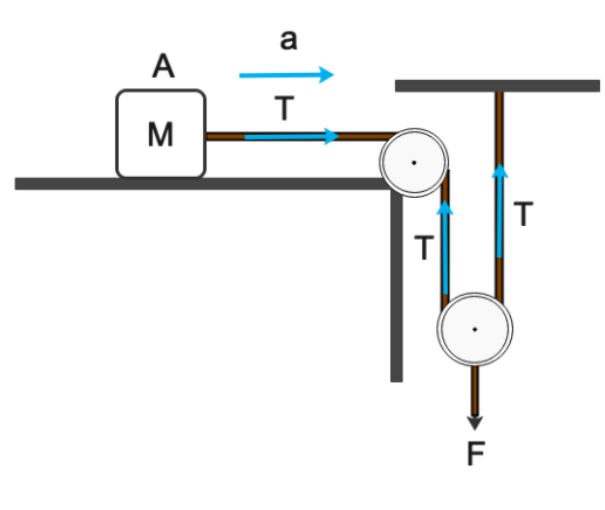
This is free body diagram of the whole system the whole system has a single rope that is why the tension in the string is same that is T
Now we will solve the question by breaking the whole system in different part and then using that we will make their free body diagram to make the equations
Free body diagram of pulley

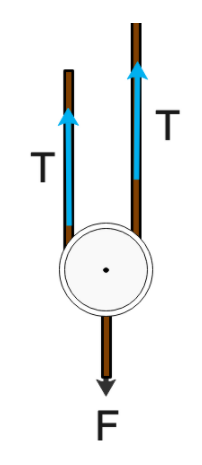
Two ropes are applying tension on the upward direction while one is applying force on downward direction
Now we will apply the formula of net force
${F_{Net}} = ma$
$F - 2T = {M_P}{a_P}$
${M_P}$ is the mass of the pulley which is zero
$\because {M_P} = 0$
$F - 2T = 0$
Taking tension on the other side
$F = 2T$
Hence tension is equal to
$T = \dfrac{F}{2}$

Free body diagram of Block - A

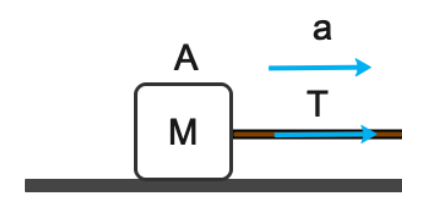
Rope is applying tension and because of acceleration is also applied in the same direction
Now we will apply the formula of net force
${F_{Net}} = ma$
$T = Ma$
Substituting the value of tension
$\dfrac{F}{2} = Ma$
Taking mass on the other side and we get the acceleration equal to
$a = \dfrac{F}{{2M}}$
Hence, the correct option $A){\text{ }}\dfrac{F}{{2M}}$.

Note:
Many of the people will make the mistake by not assuming the mass of the pulley zero as it is not mentioned in the question but these are typical types of question in which after see the options we can judge that the mass of pulley is neglected along with this tension the whole string will remain same as it doesn’t break anywhere.