Question

Prove the given inverse trigonometric ratio : $\tan \left( \dfrac{1}{2}{{\sin }^{-1}}\left( \dfrac{3}{4} \right) \right)=\dfrac{4-\sqrt{7}}{3}$.

Answer 1

We start solving this problem by first assuming that ${{\sin }^{-1}}\left( \dfrac{3}{4} \right)=\theta$. In the obtained sine function, we assume the numerator as perpendicular and denominator as hypotenuse. Then we find the base using the Pythagoras theorem given by $\text{hypotenus}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicula}{{\text{r}}^{\text{2}}}$. So, now we have to find the value of $\tan \left( \dfrac{\theta }{2} \right)$. Then we use the half angle formula $\tan \theta =\dfrac{2\tan \left( \dfrac{\theta }{2} \right)}{1-{{\tan }^{2}}\left( \dfrac{\theta }{2} \right)}$, and substitute the value of $\tan \theta$ and solve it to form a quadratic equation in $\tan \left( \dfrac{\theta }{2} \right)$. Then we use the formula for the roots of the quadratic equation $a{{x}^{2}}+bx+c=0$, $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$ and find the values of $\tan \left( \dfrac{\theta }{2} \right)$. Then we check which of the values obtained satisfy the condition ${{\sin }^{-1}}\left( \dfrac{3}{4} \right)=\theta$.

Complete step-by-step solution -
Here we need to prove that $\tan \left( \dfrac{1}{2}{{\sin }^{-1}}\left( \dfrac{3}{4} \right) \right)=\dfrac{4-\sqrt{7}}{3}$.
Let us assume that ${{\sin }^{-1}}\left( \dfrac{3}{4} \right)=\theta$. We can also write it as $\sin \theta =\dfrac{3}{4}$
Then we need to prove that, $\tan \left( \dfrac{1}{2}\theta \right)=\dfrac{4-\sqrt{7}}{3}$, that is $\tan \left( \dfrac{\theta }{2} \right)=\dfrac{4-\sqrt{7}}{3}$.
So, we need to find the value of $\tan \left( \dfrac{\theta }{2} \right)$ from $\sin \theta =\dfrac{3}{4}$.
First, let us find the value of $\tan \theta$.
We know that, $\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. On comparing we get that in $\sin \theta =\dfrac{3}{4}$, 3 is the perpendicular and 4 is the hypotenuse.

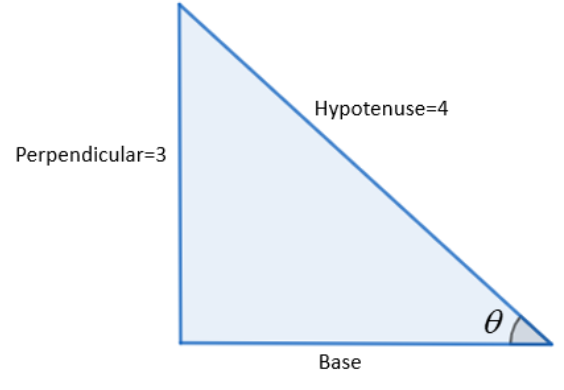
Using Pythagoras theorem given by: $\text{hypotenus}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicula}{{\text{r}}^{\text{2}}}$, we have,
$\begin{aligned} & \text{bas}{{\text{e}}^{\text{2}}}=\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}} \\\ & \Rightarrow \text{base}=\sqrt{\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}}} \\\ & \Rightarrow \text{base}=\sqrt{{{4}^{\text{2}}}-{{3}^{\text{2}}}} \\\ & \Rightarrow \text{base}=\sqrt{16-9} \\\ & \Rightarrow \text{base}=\sqrt{7} \\\ \end{aligned}$
Now, we know that, $\tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}}$.
So, we get the value of $\tan \theta$ as,
$\tan \theta =\dfrac{3}{\sqrt{7}}........\left( 1 \right)$
Now, let us consider the half angle formula
$\tan \theta =\dfrac{2\tan \left( \dfrac{\theta }{2} \right)}{1-{{\tan }^{2}}\left( \dfrac{\theta }{2} \right)}$
Now let us substitute the value of $\tan \theta$ from equation (1), in the above equation. Then we get,
$\dfrac{3}{\sqrt{7}}=\dfrac{2\tan \left( \dfrac{\theta }{2} \right)}{1-{{\tan }^{2}}\left( \dfrac{\theta }{2} \right)}$
By cross-multiplication we get,
$\begin{aligned} & 3-3{{\tan }^{2}}\left( \dfrac{\theta }{2} \right)=2\sqrt{7}\tan \left( \dfrac{\theta }{2} \right) \\\ & \Rightarrow 3{{\tan }^{2}}\left( \dfrac{\theta }{2} \right)+2\sqrt{7}\tan \left( \dfrac{\theta }{2} \right)-3=0 \\\ \end{aligned}$
Now let us consider the formula for the roots of the quadratic equation, $a{{x}^{2}}+bx+c=0$.
$x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$
Using this formula, we can write the roots of our above equation as,

& \tan \left( \dfrac{\theta }{2} \right)=\dfrac{-2\sqrt{7}\pm \sqrt{{{\left( 2\sqrt{7} \right)}^{2}}-\left( 4\times 3\times (-3) \right)}}{2\times 3} \\\ & \Rightarrow \tan \left( \dfrac{\theta }{2} \right)=\dfrac{-2\sqrt{7}\pm \sqrt{28+36}}{6} \\\ & \Rightarrow \tan \left( \dfrac{\theta }{2} \right)=\dfrac{-2\sqrt{7}\pm \sqrt{64}}{6} \\\ \end{aligned}$$ Writing the square root of 64 as 8, we get, $$\begin{aligned} & \Rightarrow \tan \left( \dfrac{\theta }{2} \right)=\dfrac{-2\sqrt{7}\pm 8}{6} \\\ & \Rightarrow \tan \left( \dfrac{\theta }{2} \right)=\dfrac{-\sqrt{7}\pm 4}{3} \\\ \end{aligned}$$ So, we get that $$\tan \left( \dfrac{\theta }{2} \right)=\dfrac{-\sqrt{7}+4}{3}\text{ or }\tan \left( \dfrac{\theta }{2} \right)=\dfrac{-\sqrt{7}-4}{3}$$. Since, $\sin \theta =\dfrac{3}{4}$ is positive, therefore, $\theta $ must be lying in the first or second quadrant, that is, $0<\theta $ $<{{180}^{\circ }}$ Then we get the range of $\left( \dfrac{\theta }{2} \right)$ as $0<\left( \dfrac{\theta }{2} \right)<{{90}^{\circ }}$. Hence, $\left( \dfrac{\theta }{2} \right)$ must lie in the first quadrant. So, $\tan \left( \dfrac{\theta }{2} \right)$ must be positive. Hence, the only value of $$\tan \left( \dfrac{\theta }{2} \right)=\dfrac{4-\sqrt{7}}{3}$$. So, we get that $\tan \left( \dfrac{1}{2}{{\sin }^{-1}}\left( \dfrac{3}{4} \right) \right)=\dfrac{4-\sqrt{7}}{3}$. Hence Proved. **Note:** There are many alternate ways to solve this question. We can convert the given sine inverse functions into cosine inverse function by taking the ratio of base and hypotenuse and then apply the formula $${{\tan }^{2}}\left( \dfrac{\theta }{2} \right)=\dfrac{1-\cos \theta }{1+\cos \theta }$$, to get the answer. Here we have above that, $\sin \theta =\dfrac{3}{4}$ We have also got that base is $\sqrt{7}$ and perpendicular is 3 and the hypotenuse is 4. As, $\cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}}$, we get that $\cos \theta =\dfrac{\sqrt{7}}{4}$. Now, let us substitute this value in the formula, $${{\tan }^{2}}\left( \dfrac{\theta }{2} \right)=\dfrac{1-\cos \theta }{1+\cos \theta }$$. Then we get, $$\begin{aligned} & \Rightarrow {{\tan }^{2}}\left( \dfrac{\theta }{2} \right)=\dfrac{1-\dfrac{\sqrt{7}}{4}}{1+\dfrac{\sqrt{7}}{4}} \\\ & \Rightarrow {{\tan }^{2}}\left( \dfrac{\theta }{2} \right)=\dfrac{4-\sqrt{7}}{4+\sqrt{7}} \\\ \end{aligned}$$ Multiplying numerator and denominator with $$4-\sqrt{7}$$, we get, $$\begin{aligned} & \Rightarrow {{\tan }^{2}}\left( \dfrac{\theta }{2} \right)=\dfrac{4-\sqrt{7}}{4+\sqrt{7}}\times \dfrac{4-\sqrt{7}}{4-\sqrt{7}} \\\ & \Rightarrow {{\tan }^{2}}\left( \dfrac{\theta }{2} \right)=\dfrac{{{\left( 4-\sqrt{7} \right)}^{2}}}{16-7} \\\ \end{aligned}$$ $$\begin{aligned} & \Rightarrow {{\tan }^{2}}\left( \dfrac{\theta }{2} \right)=\dfrac{{{\left( 4-\sqrt{7} \right)}^{2}}}{9} \\\ & \Rightarrow \tan \left( \dfrac{\theta }{2} \right)=\pm \dfrac{4-\sqrt{7}}{3} \\\ \end{aligned}$$ Since, $\sin \theta =\dfrac{3}{4}$ is positive, therefore, $\theta $ must be lying in the first or second quadrant, that is, $0<\theta $ $<{{180}^{\circ }}$ Then we get the range of $\left( \dfrac{\theta }{2} \right)$ as $0<\left( \dfrac{\theta }{2} \right)<{{90}^{\circ }}$. Hence, $\left( \dfrac{\theta }{2} \right)$ must lie in the first quadrant. So, $\tan \left( \dfrac{\theta }{2} \right)$ must be positive. Hence, the only value of $$\tan \left( \dfrac{\theta }{2} \right)=\dfrac{4-\sqrt{7}}{3}$$.