Question

Prove the given inverse trigonometric expression: $\tan \left( \dfrac{1}{2}{{\sin }^{-1}}\left( \dfrac{3}{4} \right) \right)=\dfrac{4-\sqrt{7}}{3}$.

Answer 1

Hint: Assume, ${{\sin }^{-1}}\left( \dfrac{3}{4} \right)=\theta$. Convert this sine inverse function into tan inverse function. In the given sine inverse function, assume the numerator as perpendicular and denominator as hypotenuse. Find the base using Pythagoras theorem given by: $\text{(hypotenuse)}^{2}=\text{(base)}^{2}+\text{(perpendicular)}^{2}$. So, now we have to find the value of $\tan \left( \dfrac{\theta }{2} \right)$. Use the half angle formula: $\tan \theta =\dfrac{2\tan \left( \dfrac{\theta }{2} \right)}{1-{{\tan }^{2}}\left( \dfrac{\theta }{2} \right)}$, to form a quadratic equation in $\tan \left( \dfrac{\theta }{2} \right)$ by substituting the value of $\tan \theta$. Now, solve this quadratic equation to get the answer.

Complete step-by-step solution -
Let us assume: ${{\sin }^{-1}}\left( \dfrac{3}{4} \right)=\theta$.
We know that, $\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$, therefore, $\theta ={{\sin }^{-1}}\left( \dfrac{\text{Perpendicular}}{\text{Hypotenuse}} \right)$. On comparing we get that, in ${{\sin }^{-1}}\left( \dfrac{3}{4} \right)$, 3 is the perpendicular and 4 is the hypotenuse.

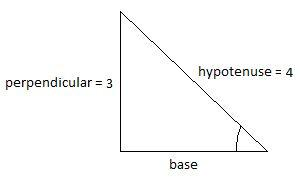
Using Pythagoras theorem given by: $\text{(hypotenuse)}^{2}=\text{(base)}^{2}+\text{(perpendicular)}^{2}$, we have,
$\begin{aligned} & \text{(base)}^{2}=\text{(hypotenuse)}^{2}-\text{(perpendicular)}^{2} \\\ & \Rightarrow \text{base}=\sqrt{\text{(hypotenuse)}^{2}-\text{(perpendicular)}^{2}} \\\ & \Rightarrow \text{base}=\sqrt{{{4}^{\text{2}}}-{{3}^{\text{2}}}} \\\ & \Rightarrow \text{base}=\sqrt{16-9} \\\ & \Rightarrow \text{base}=\sqrt{7} \\\ \end{aligned}$
Now, we know that, $\tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}}$, therefore, $\theta ={{\tan }^{-1}}\left( \dfrac{\text{Perpendicular}}{\text{Base}} \right)$.
$\Rightarrow {{\sin }^{-1}}\left( \dfrac{3}{4} \right)={{\tan }^{-1}}\left( \dfrac{3}{\sqrt{7}} \right)$
Since, we have assumed, ${{\sin }^{-1}}\left( \dfrac{3}{4} \right)=\theta$.
$\begin{aligned} & \Rightarrow {{\tan }^{-1}}\left( \dfrac{3}{\sqrt{7}} \right)=\theta \\\ & \Rightarrow \tan \theta =\dfrac{3}{\sqrt{7}}..................(i) \\\ \end{aligned}$
Now, the expression: $\tan \left( \dfrac{1}{2}{{\sin }^{-1}}\left( \dfrac{3}{4} \right) \right)$ becomes $\tan \left( \dfrac{\theta }{2} \right)$.
Now, applying the half angle formula: $\tan \theta =\dfrac{2\tan \left( \dfrac{\theta }{2} \right)}{1-{{\tan }^{2}}\left( \dfrac{\theta }{2} \right)}$, and substituting the value of $\tan \theta$ from equation (i), we get,
$\dfrac{3}{\sqrt{7}}=\dfrac{2\tan \left( \dfrac{\theta }{2} \right)}{1-{{\tan }^{2}}\left( \dfrac{\theta }{2} \right)}$
By cross-multiplication we get,
$\begin{aligned} & 3-3{{\tan }^{2}}\left( \dfrac{\theta }{2} \right)=2\sqrt{7}\tan \left( \dfrac{\theta }{2} \right) \\\ & \Rightarrow 3{{\tan }^{2}}\left( \dfrac{\theta }{2} \right)+2\sqrt{7}\tan \left( \dfrac{\theta }{2} \right)-3=0 \\\ \end{aligned}$
Solving this quadratic equation by discriminant method, we get,

& \tan \left( \dfrac{\theta }{2} \right)=\dfrac{-2\sqrt{7}\pm \sqrt{{{\left( 2\sqrt{7} \right)}^{2}}-4\times 3\times (-3)}}{2\times 3} \\\ & \Rightarrow \tan \left( \dfrac{\theta }{2} \right)=\dfrac{-2\sqrt{7}\pm \sqrt{28+36}}{6} \\\ & \Rightarrow \tan \left( \dfrac{\theta }{2} \right)=\dfrac{-2\sqrt{7}\pm \sqrt{64}}{6} \\\ & \Rightarrow \tan \left( \dfrac{\theta }{2} \right)=\dfrac{-2\sqrt{7}\pm 8}{6} \\\ & \Rightarrow \tan \left( \dfrac{\theta }{2} \right)=\dfrac{-\sqrt{7}\pm 4}{3} \\\ & \text{either }\tan \left( \dfrac{\theta }{2} \right)=\dfrac{-\sqrt{7}+4}{3}\text{ or }\tan \left( \dfrac{\theta }{2} \right)=\dfrac{-\sqrt{7}-4}{3} \\\ \end{aligned}$$ Since, $\sin \theta $ is positive, therefore, $\theta $ must be lying in the first quadrant. Hence, $\left( \dfrac{\theta }{2} \right)$ must lie in the first quadrant. So, $\tan \left( \dfrac{\theta }{2} \right)$ must be positive. Hence, the only value of $$\tan \left( \dfrac{\theta }{2} \right)=\dfrac{4-\sqrt{7}}{3}$$. Note: There are many alternate ways to solve this question. We can convert the given sine inverse functions, in the L.H.S, to any of the desired inverse functions and then use the Pythagoras theorem to get the answer. Here, we have changed it in tan inverse function. You may change it in cosine inverse function by taking the ratio of base and hypotenuse and then apply the formula: $${{\tan }^{2}}\left( \dfrac{\theta }{2} \right)=\dfrac{1-\cos \theta }{1+\cos \theta }$$, to get the answer.