Question

Prove the given expression, $\cos [ta{{n}^{-1}}\\{sin(co{{t}^{-1}}x)\\}]=\sqrt{\dfrac{1+{{x}^{2}}}{2+{{x}^{2}}}}$ .

Answer 1

Hint: In this question, we have multiple trigonometric functions. So we have to do trigonometric conversion multiple times. We have inverse tan function and inverse cot function. Assume, $\theta ={{\cot }^{-1}}x$ and then transform $\cot \theta$ into $\sin \theta$ . Also assume $\beta ={{\tan }^{-1}}\left( \dfrac{1}{\sqrt{1+{{x}^{2}}}} \right)$ and then transform $\tan \beta$ into $\cos \beta$ . Now, it can be solved easily.

Complete step-by-step solution -
Solve this question, step by step.
Treat $\sin (co{{t}^{-1}}x)$ as the first part and then simplify this.
So, first of all, we have to solve $\sin (co{{t}^{-1}}x)$.
Let us assume,
$\theta ={{\cot }^{-1}}x$
$\Rightarrow \cot \theta =x$…………..(1)
We have, $\cot \theta =\dfrac{\text{base}}{\text{Height}}$,

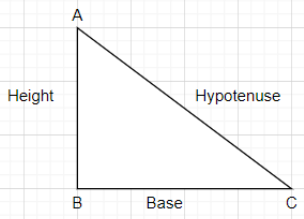
Base = x,
Height= 1,
Using Pythagoras theorem Hypotenuse =$\sqrt{{{\left(\text{height} \right)}^{2}}+{{\left(\text{Base} \right)}^{2}}}$, we get
Hypotenuse= $\sqrt{1+{{x}^{2}}}$
$\sin \theta =\dfrac{\text{height}}{\text{hypotenuse}}$
$\sin \theta =\dfrac{1}{\sqrt{1+{{x}^{2}}}}$
$\Rightarrow \theta ={{\sin }^{-1}}\left( \dfrac{1}{\sqrt{1+{{x}^{2}}}} \right)$………………(2)
According to the question, we have \cos [ta{{n}^{-1}}{\sin({\cot}^{-1}}x)\\}]………….(3)
From equation(1), we have $\theta ={{\cot }^{-1}}x$ .
Substituting equation(1) in equation(3), we get $\cos [ta{{n}^{-1}}\\{sin\theta \\}]$…………..(4)
Now, using equation(2), equation(4) can be written as

& \sin ({{\sin }^{-1}}\left( \dfrac{1}{\sqrt{1+{{x}^{2}}}} \right)) \\\ & =\dfrac{1}{\sqrt{1+{{x}^{2}}}} \\\ \end{aligned}$$ Our equation may be written as, $$\begin{aligned} & \cos \left[ {{\tan }^{-1}}\left\\{ \sin \left( {{\sin }^{-1}}\left( \dfrac{1}{\sqrt{1+{{x}^{2}}}} \right) \right) \right\\} \right] \\\ & =\cos \left[ {{\tan }^{-1}}\left( \dfrac{1}{\sqrt{1+{{x}^{2}}}} \right) \right] \\\ \end{aligned}$$ We have simplified our equation given in the question. Now, we have to solve the equation, $$\cos \left[ {{\tan }^{-1}}\left( \dfrac{1}{\sqrt{1+{{x}^{2}}}} \right) \right]$$……….(5) For this, we have to convert the inverse tan function into inverse cosine function. Similarly, let us assume, $$\beta ={{\tan }^{-1}}\left( \dfrac{1}{\sqrt{1+{{x}^{2}}}} \right)$$……………..(6) Solving equation(6), we get $$\tan \beta =\dfrac{1}{\sqrt{1+{{x}^{2}}}}$$…………..(7) We also know the identity, $${{\sec }^{2}}\beta -{{\tan }^{2}}\beta =1$$ . $$\sec \beta =\sqrt{1+{{\tan }^{2}}\beta }$$……………..(8) Using equation(7) and substituting it in equation(8), we get $$\begin{aligned} & \sec \beta =\sqrt{1+{{\tan }^{2}}\beta } \\\ & =\sqrt{1+\dfrac{1}{1+{{x}^{2}}}} \\\ & =\sqrt{\dfrac{1+{{x}^{2}}+1}{1+{{x}^{2}}}} \\\ & =\sqrt{\dfrac{2+{{x}^{2}}}{1+{{x}^{2}}}} \\\ \end{aligned}$$ We also know that, $$\cos \beta =\dfrac{1}{\sec \beta }$$ . Using this formula we can find $$\cos \beta$$ . $$\cos \beta =\dfrac{\sqrt{1+{{x}^{2}}}}{\sqrt{2+{{x}^{2}}}}$$…………….(9) Substituting equation(6) in equation(5), we get $$\cos (ta{{n}^{-1}}\left( \dfrac{1}{\sqrt{1+{{x}^{2}}}} \right))$$ $$=\cos \beta $$ Substituting the value from equation(9), we get $$\cos \beta =\sqrt{\dfrac{1+{{x}^{2}}}{2+{{x}^{2}}}}$$ Therefore,LHS=RHS Hence, proved. Note: In this question, we have to transform one trigonometric function into other trigonometric functions multiple times. So, one can easily make a mistake in the calculations involved in the transformation. It will be easier if we transform the functions using the right-angled triangle and Pythagoras theorem.  Pythagoras theorem, Hypotenuse =$$\sqrt{{{\left( \text{height} \right)}^{2}}+{{\left(\text{Base}\right)}^{2}}}$$ . Using this formula, we can find height, base and hypotenuse. Now, transformation can be done easily.