Solveeit Logo
Login

Question

Question: Prove the following. \[\tan \dfrac{11\pi }{3}-2\sin \dfrac{4\pi }{6}-\dfrac{3}{4}{{\operatorname{c...

Prove the following.
tan⁡11π3−2sin⁡4π6−34cosec⁡2π4+4cos⁡2π4+4cos⁡217π6=3−432\tan \dfrac{11\pi }{3}-2\sin \dfrac{4\pi }{6}-\dfrac{3}{4}{{\operatorname{cosec}}^{2}}\dfrac{\pi }{4}+4{{\cos }^{2}}\dfrac{\pi }{4}+4{{\cos }^{2}}\dfrac{17\pi }{6}=\dfrac{3-4\sqrt{3}}{2}

Explanation

Solution

In this question, we need to prove the given trigonometric functions to be equal to 3−432.\dfrac{3-4\sqrt{3}}{2}. For this, we first need to understand the signs of trigonometric functions in the different quadrants. Then we will use the following known values of trigonometric functions to get the final answer.
(i)sin⁡π4=12\left( i \right)\sin \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}
(ii)cosec⁡θ=1sin⁡θ\left( ii \right)\operatorname{cosec}\theta =\dfrac{1}{\sin \theta }
(iii)tan⁡π3=3\left( iii \right)\tan \dfrac{\pi }{3}=\sqrt{3}
(iv)sin⁡π3=32\left( iv \right)\sin \dfrac{\pi }{3}=\dfrac{\sqrt{3}}{2}
(v)cos⁡π6=32\left( v \right)\cos \dfrac{\pi }{6}=\dfrac{\sqrt{3}}{2}

Complete step-by-step answer:
Here, we need to prove tan⁡11π3−2sin⁡4π6−34cosec⁡2π4+4cos⁡2π4+4cos⁡217π6=3−432.\tan \dfrac{11\pi }{3}-2\sin \dfrac{4\pi }{6}-\dfrac{3}{4}{{\operatorname{cosec}}^{2}}\dfrac{\pi }{4}+4{{\cos }^{2}}\dfrac{\pi }{4}+4{{\cos }^{2}}\dfrac{17\pi }{6}=\dfrac{3-4\sqrt{3}}{2}. But first let us understand the effect on values of trigonometric function when we change the quadrant. When we add or subtract π\pi from the angle of any trigonometric function, the trigonometric function remains the same but the sign varies as per quadrant. The different trigonometric functions possess different signs in different quadrants.

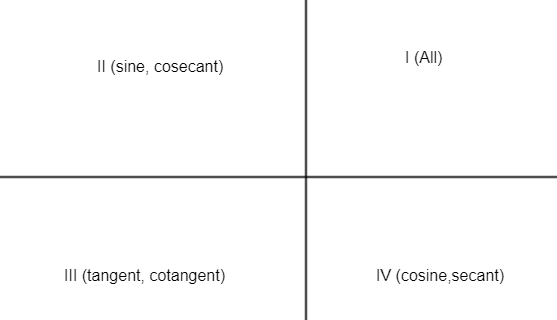
In the first quadrant, all trigonometric functions are positive. In the second quadrant, only sin and cosec functions are positive. In the third quadrant, only tan and cot functions are positive. In the fourth quadrant, only cos and sec functions are positive. Now, let us separate the terms individually and evaluate tan⁡11π3.\tan \dfrac{11\pi }{3}. It can be written as tan⁡(2π+5π3).\tan \left( 2\pi +\dfrac{5\pi }{3} \right). After the first revolution, it will remain in the same quadrant, hence it becomes equal to tan⁡5π3.\tan \dfrac{5\pi }{3}. It can be written as tan⁡(π+2π3).\tan \left( \pi +\dfrac{2\pi }{3} \right). After adding π\pi tan moves to the third quadrant where it is positive, so it becomes tan⁡2π3.\tan \dfrac{2\pi }{3}. It can be written as tan⁡(π−π3).\tan \left( \pi -\dfrac{\pi }{3} \right). Now, π−π3\pi -\dfrac{\pi }{3} will lie in the second quadrant, so tan becomes negative. Hence, we get, −tan⁡π3.-\tan \dfrac{\pi }{3}. We know that tan⁡π3=3.\tan \dfrac{\pi }{3}=\sqrt{3}. Hence,
tan⁡11π3=−3......(i)\tan \dfrac{11\pi }{3}=-\sqrt{3}......\left( i \right)
(ii)sin⁡4π6\left( ii \right)\sin \dfrac{4\pi }{6}
It can be written as 2π3\dfrac{2\pi }{3} which can be further written as π−π3.\pi -\dfrac{\pi }{3}. So, we get, sin⁡(π−π3).\sin \left( \pi -\dfrac{\pi }{3} \right). Now, it will lie in the second quadrant where it is positive, so, sin⁡(π−π3)=sin⁡π3.\sin \left( \pi -\dfrac{\pi }{3} \right)=\sin \dfrac{\pi }{3}. Since, sin⁡π3=32.\sin \dfrac{\pi }{3}=\dfrac{\sqrt{3}}{2}. So, sin⁡4π6=32.....(ii)\sin \dfrac{4\pi }{6}=\dfrac{\sqrt{3}}{2}.....\left( ii \right)
(iii)cosec⁡2π4\left( iii \right){{\operatorname{cosec}}^{2}}\dfrac{\pi }{4}
We know that cosec⁡θ=1sin⁡θ\operatorname{cosec}\theta =\dfrac{1}{\sin \theta } and sin⁡π4=12,\sin \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}, so cosec⁡2π4=1sin⁡2π4=1(12)2=(2)2=2.{{\operatorname{cosec}}^{2}}\dfrac{\pi }{4}=\dfrac{1}{{{\sin }^{2}}\dfrac{\pi }{4}}=\dfrac{1}{{{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}}}={{\left( \sqrt{2} \right)}^{2}}=2.
Hence, cosec⁡2π4=2......(iii){{\operatorname{cosec}}^{2}}\dfrac{\pi }{4}=2......\left( iii \right)
(iv)cos⁡217π6\left( iv \right){{\cos }^{2}}\dfrac{17\pi }{6}
It can be written as cos⁡(2π+5π6),\cos \left( 2\pi +\dfrac{5\pi }{6} \right), the sign remains the same after the full revolution. So, we get, cos⁡5π6.\cos \dfrac{5\pi }{6}. It can be written as cos⁡(π−π6).\cos \left( \pi -\dfrac{\pi }{6} \right). Now, it will lie in the second quadrant, so we get −cos⁡π6.\dfrac{-\cos \pi }{6}. Since, cos⁡π6=32.\cos \dfrac{\pi }{6}=\dfrac{\sqrt{3}}{2}. So,
cos⁡17π6=−32......(iv)\cos \dfrac{17\pi }{6}=\dfrac{-\sqrt{3}}{2}......\left( iv \right)
Now our equation was
tan⁡11π3−2sin⁡4π6−34cosec⁡2π4+4cos⁡2π4+4cos⁡217π6=3−432\tan \dfrac{11\pi }{3}-2\sin \dfrac{4\pi }{6}-\dfrac{3}{4}{{\operatorname{cosec}}^{2}}\dfrac{\pi }{4}+4{{\cos }^{2}}\dfrac{\pi }{4}+4{{\cos }^{2}}\dfrac{17\pi }{6}=\dfrac{3-4\sqrt{3}}{2}
Putting values from (i), (ii), (iii) and (iv), we get,
⇒−3−2(32)−34(2)+4(−32)2=3−432\Rightarrow -3-2\left( \dfrac{\sqrt{3}}{2} \right)-\dfrac{3}{4}\left( 2 \right)+4{{\left( \dfrac{-\sqrt{3}}{2} \right)}^{2}}=\dfrac{3-4\sqrt{3}}{2}
⇒−3−3−32+4(34)=3−432\Rightarrow -\sqrt{3}-\sqrt{3}-\dfrac{3}{2}+4\left( \dfrac{3}{4} \right)=\dfrac{3-4\sqrt{3}}{2}
⇒−23−32+3=3−432\Rightarrow -2\sqrt{3}-\dfrac{3}{2}+3=\dfrac{3-4\sqrt{3}}{2}
Taking 2 common, we get,
⇒−43−3+62=3−432\Rightarrow \dfrac{-4\sqrt{3}-3+6}{2}=\dfrac{3-4\sqrt{3}}{2}
⇒3−432=3−432\Rightarrow \dfrac{3-4\sqrt{3}}{2}=\dfrac{3-4\sqrt{3}}{2}
Hence proved.

Note: Students should take care of the signs while evaluating all these values. If we take an angle as 90∘+θ{{90}^{\circ }}+\theta or 90∘−θ,{{90}^{\circ }}-\theta , then the trigonometric function also changes. For example, cos⁡(90∘−θ)=sin⁡θ.\cos \left( {{90}^{\circ }}-\theta \right)=\sin \theta . The cos⁡θ\cos \theta changes to sin⁡θ\sin \theta and vice versa and tan⁡θ\tan \theta changes to cot⁡θ\cot \theta and vice versa. We need to take care while adding or subtracting rational numbers with irrational numbers.