Question
Question: Prove the following expression: \[\underset{n\to \infty }{\mathop{\lim \text{it}}}\,\dfrac{1}{n}\...
Prove the following expression:
n→∞limitn1[cos2p2nπ+cos2p2n2π+cos2p2n3π+cos2p2π]=r=1∏p4rp+r
Solution
Hint: Apply reverse of limit as a sum means converting any infinite series to integral form. Find ∫02πcosnxdx using integration by parts by splitting cosnx to cosx and cosn−1x.
Here, we have the limit given to calculate is
n→∞limn1[cos2p2nπ+cos2p2n2π+cos2p2n3π+......cos2p2nnπ]which should be equal to given result r=1∏p4rp+ri.e.,
(4p+1)(4.2p+2)(4.3p+3)......(4.p2p)
Let us first calculate LHS part of the given equation;
n→∞limn1[cos2p2nπ+cos2p2n2π+cos2p2n3π+......cos2p2nnπ]..........(1)
Here, we can put a direct limit to the function, and we cannot find summation of the given series (very complex). We cannot put a limit because the number of times is not defined.
So, here we need to apply limits as a sum rule of integration.
Basic definition of limit as a sum that if we want to find integration of any function then we can break that function into infinite sums;
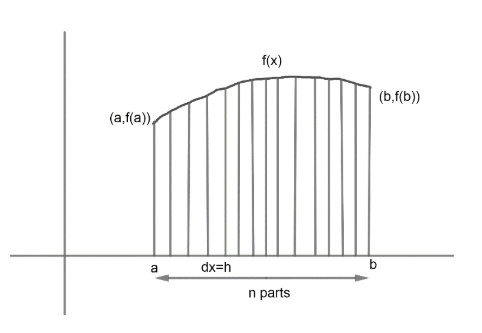
(h=nb−a)
We can write ∫abf(x)dx to sum of area of very short intervals of length ‘h’, and can be expressed
∫abf(x)dx=hf(a)+hf(a+h)+hf(a+2h)+....hf(a+(n−1)h)
Where h(f(a)), hf(a+h)………hf(a+(n-1)h) are areas of rectangles formed.
∫abf(x)dx=(b−a)n→∞limn1(f(a)+f(a+h)+.......f(a+(n−1)d))
We can observe that reverse of the limit as a sum of integration should also be true and expressed as follows;
Above given series can be written as;
∫abf(x)dx=n→∞limnb−ar=0∑nf(a+rh)
We have, h=nb−a
∫abf(x)dx=h→0limhr=0∑n=h(b−a)f(a+rh)
By comparison, of the above equation, we can get the reverse of the above as well.
Let us suppose we have series given as;
