Question

Prove the following:
$\dfrac{\cos \left( \pi +\theta \right)\cos \left( -\theta \right)}{\sin \left( \pi -\theta \right)\cos \left( \dfrac{\pi }{2}+\theta \right)}={{\cot }^{2}}\theta$

Answer 1

Hint: We will be using the concepts of trigonometric function to solve the problem. We will be using the trigonometric formulae like:

& \cos \left( \pi +\theta \right)=-\cos \theta \\\ & \cos \left( -\theta \right)=\cos \theta \\\ & \sin \left( \pi -\theta \right)=\sin \theta \\\ & \cos \left( \dfrac{\pi }{2}+\theta \right)=-\sin \theta \\\ & \dfrac{\cos \theta }{\sin \theta }=\cot \theta \\\ \end{aligned}$$ _Complete step-by-step answer:_ Now, we have to prove that, $\dfrac{\cos \left( \pi +\theta \right)\cos \left( -\theta \right)}{\sin \left( \pi -\theta \right)\cos \left( \dfrac{\pi }{2}+\theta \right)}={{\cot }^{2}}\theta $ Now, we know that for trigonometric ratios of supplementary angles are determined as, 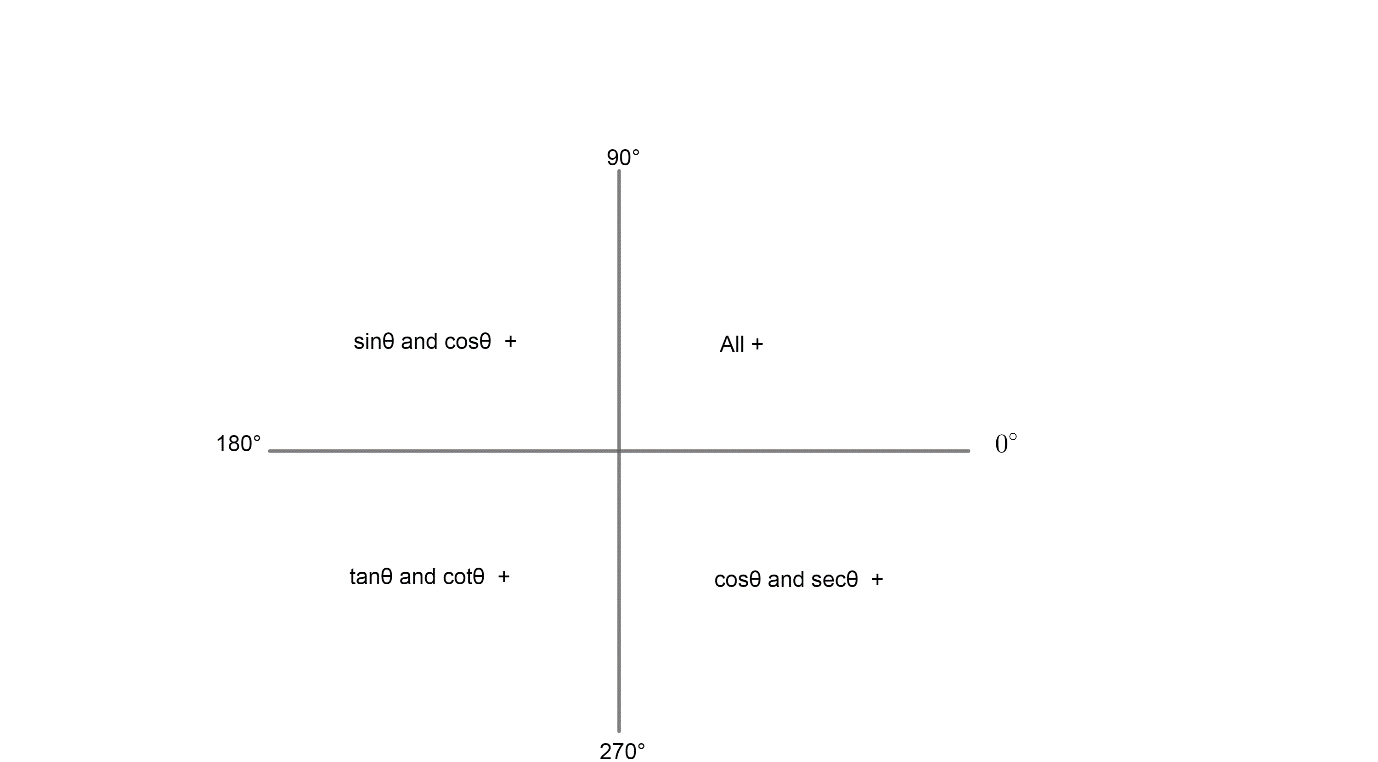 The figure shows the quadrant in which the trigonometric ratios are positive. Now, it is important to note that the trigonometric ratio of an angle and its supplement is the same in magnitude but the sign depends on the quadrant in which it lies. For example: $\sin \left( 180-\theta \right)=\sin \left( \theta \right)$ as sin is positive in the second quadrant. Now, the same goes for complementary angles but in those the co-functions are the same and the sign depends on the quadrant in which the trigonometric function lies. For example: $$\sin \left( 90-\theta \right)=\cos \theta $$. Now, we take LHS, $\dfrac{\cos \left( \pi +\theta \right)\cos \left( -\theta \right)}{\sin \left( \pi -\theta \right)\cos \left( \dfrac{\pi }{2}+\theta \right)}$ Now, we have, $$\begin{aligned} & \cos \left( \pi +\theta \right)=-\cos \theta \\\ & \cos \left( -\theta \right)=\cos \theta \\\ & \sin \left( \pi -\theta \right)=\sin \theta \\\ & \cos \left( \dfrac{\pi }{2}+\theta \right)=-\sin \theta \\\ \end{aligned}$$ So, the LHS become, $\begin{aligned} & \dfrac{-\cos \theta \times \cos \theta }{\sin \theta \times \left( -\sin \theta \right)} \\\ & =\dfrac{{{\cos }^{2}}\theta }{{{\sin }^{2}}\theta } \\\ \end{aligned}$ Now, we know that $\dfrac{\cos \theta }{\sin \theta }=\cot \theta $. Therefore, we have, $\dfrac{\cos \left( \pi +\theta \right)\cos \left( -\theta \right)}{\sin \left( \pi -\theta \right)\cos \left( \dfrac{\pi }{2}+\theta \right)}={{\cot }^{2}}\theta $ Now, since LHS = RHS Hence proved. Note: To solve these type of questions it is important to note that we have used the ASTC quadrant system in which all the trigonometric ratios are positive in the first quadrant whereas only sine, cosec is positive in the second quadrant and tan, cot is positive in the third quadrant and cos, sec is positive in the fourth quadrant like 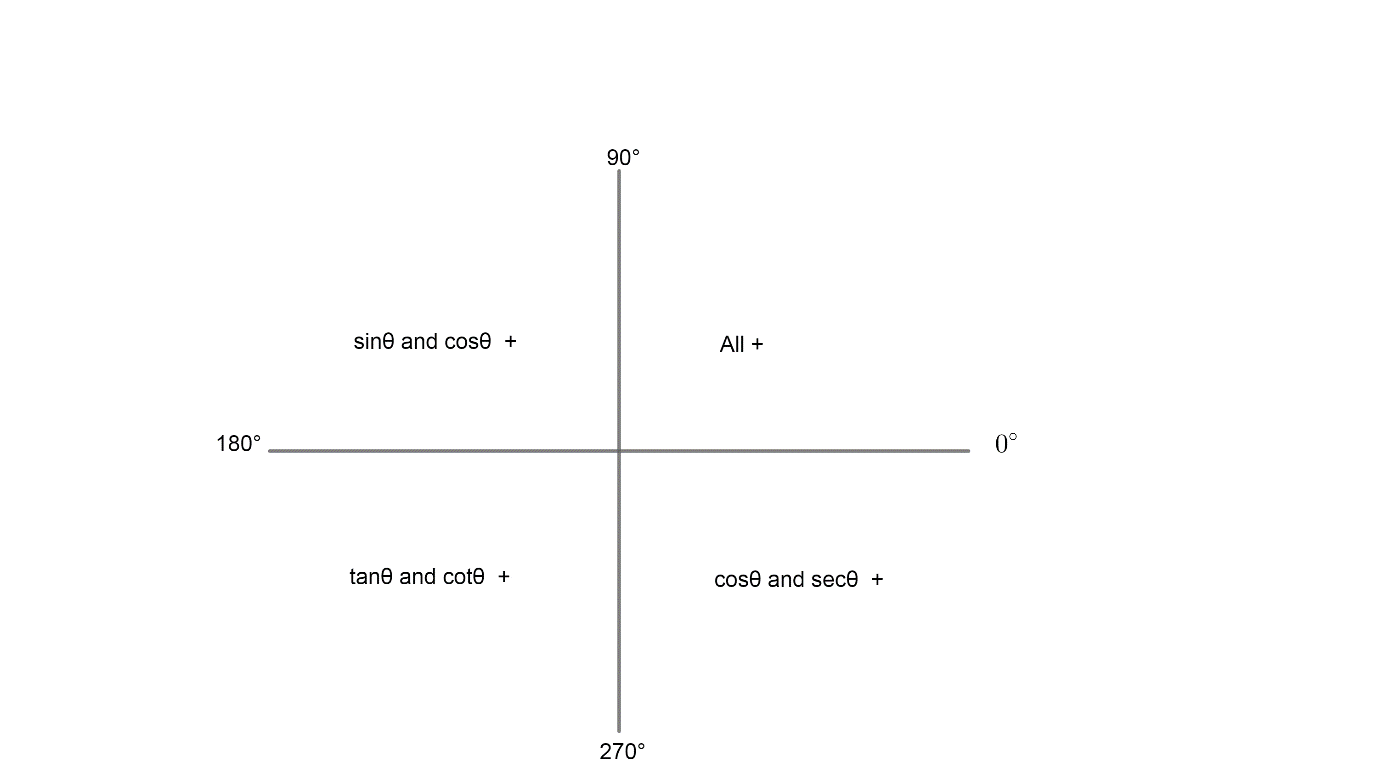 also it is important to remember the trigonometric formula like: $$\begin{aligned} & \cos \left( \pi +\theta \right)=-\cos \theta \\\ & \sin \left( \dfrac{\pi }{2}+\theta \right)=\cos \left( \theta \right) \\\ & \cos \left( \dfrac{\pi }{2}+\theta \right)=-\cos \theta \\\ \end{aligned}$$ Hence, remembering these formulae will help to shorten the solution.