Question

Prove the following:
$\cot 4x\left( {\sin 5x + \sin 3x} \right) = \cot x\left( {\sin 5x - \sin 3x} \right)$

Answer 1

We can take the LHS of the given equation and simplify it using the trigonometric identity$\sin \left( A \right) + \sin \left( B \right) = 2\sin \left( {\dfrac{{A + B}}{2}} \right)\cos \left( {\dfrac{{A - B}}{2}} \right)$.We can also take the RHS and then use the identity $\sin \left( A \right) - \sin \left( B \right) = 2\cos \left( {\dfrac{{A + B}}{2}} \right)\sin \left( {\dfrac{{A - B}}{2}} \right)$ to simplify it. On doing further calculations, we will obtain a simple form of LHS and RHS. We can prove the given equation by comparing LHS and RHS and prove they are equal.

Complete step by step Answer:

We need to prove that$\cot 4x\left( {\sin 5x + \sin 3x} \right) = \cot x\left( {\sin 5x - \sin 3x} \right)$
Let us look at the LHS,
$LHS = \cot 4x\left( {\sin 5x + \sin 3x} \right)$
We can add the terms inside the bracket of the LHS.
We know that $\sin \left( A \right) + \sin \left( B \right) = 2\sin \left( {\dfrac{{A + B}}{2}} \right)\cos \left( {\dfrac{{A - B}}{2}} \right)$
We can substitute the values,
$\Rightarrow \sin \left( {5x} \right) + \sin \left( {3x} \right) = 2\sin \left( {\dfrac{{5x + 3x}}{2}} \right)\cos \left( {\dfrac{{5x - 3x}}{2}} \right)$
On simplification, we get,
$\Rightarrow \sin \left( {5x} \right) + \sin \left( {3x} \right) = 2\sin \left( {4x} \right)\cos \left( x \right)$
We can substitute it in the LHS.
$\Rightarrow LHS = \cot 4x\left( {2\sin 4x\cos x} \right)$
We know that $\cot A = \dfrac{{\cos A}}{{\sin A}}$, so the LHS becomes,
$\Rightarrow LHS = \dfrac{{\cos 4x}}{{\sin 4x}}\left( {2\sin 4x\cos x} \right)$
On simplification, we get,
$\Rightarrow LHS = 2\cos 4x\cos x$ … (1)
Now we can take the RHS,
$RHS = \cot x\left( {\sin 5x - \sin 3x} \right)$
We know that, $\sin \left( A \right) - \sin \left( B \right) = 2\cos \left( {\dfrac{{A + B}}{2}} \right)\sin \left( {\dfrac{{A - B}}{2}} \right)$
We can substitute the values,
$\Rightarrow \sin \left( {5x} \right) - \sin \left( {3x} \right) = 2\cos \left( {\dfrac{{5x + 3x}}{2}} \right)\sin \left( {\dfrac{{5x - 3x}}{2}} \right)$
On simplification, we get,
$\Rightarrow \sin \left( {5x} \right) - \sin \left( {3x} \right) = 2\cos \left( {4x} \right)\sin \left( x \right)$
We can substitute it in the RHS.
$\Rightarrow RHS = \cot x\left( {2\cos 4x\sin x} \right)$
We know that $\cot A = \dfrac{{\cos A}}{{\sin A}}$, so the RHS becomes,
$\Rightarrow RHS = \dfrac{{\cos x}}{{\sin x}}\left( {2\cos 4x\sin x} \right)$
On simplification, we get,
$\Rightarrow RHS = 2\cos 4x\cos x$ … (2)
On comparing (1) and (2), we can conclude that both LHS and RHS are equal,
$\Rightarrow LHS = RHS$.
Hence the equation is proved.

Note: We must be familiar to the following trigonometric identities used in this problem.
$\cos \left( A \right) + \cos \left( B \right) = 2\cos \left( {\dfrac{{A + B}}{2}} \right)\cos \left( {\dfrac{{A - B}}{2}} \right)$
$\cos \left( A \right) - \cos \left( B \right) = - 2\sin \left( {\dfrac{{A + B}}{2}} \right)\sin \left( {\dfrac{{A - B}}{2}} \right)$
$\sin \left( A \right) + \sin \left( B \right) = 2\sin \left( {\dfrac{{A + B}}{2}} \right)\cos \left( {\dfrac{{A - B}}{2}} \right)$
$\sin \left( A \right) - \sin \left( B \right) = 2\cos \left( {\dfrac{{A + B}}{2}} \right)\sin \left( {\dfrac{{A - B}}{2}} \right)$
$\sin \left( { - x} \right) = - \sin \left( x \right)$
$\cos \left( { - x} \right) = \cos \left( x \right)$
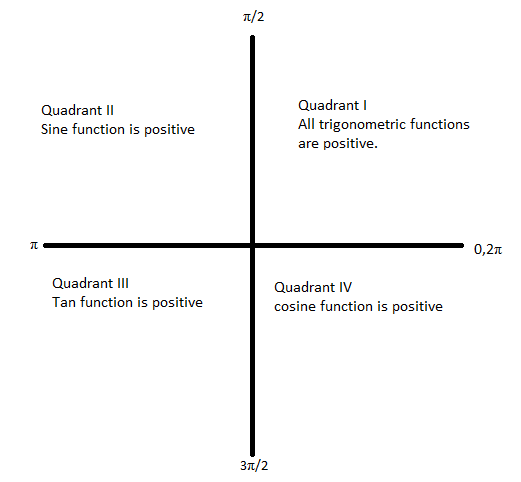
We must know the values of trigonometric functions at common angles. Adding $\pi$or multiples of $\pi$with the angle retains the ratio and adding $\dfrac{\pi }{2}$or odd multiples of $\dfrac{\pi }{2}$will change the ratio. While converting the angles we must take care of the sign of the ratio in its respective quadrant. In the 1st quadrant all the trigonometric ratios are positive. In the 2nd quadrant only sine and sec are positive. In the third quadrant, only tan and cot are positive and in the fourth quadrant, only cos and sec are positive. The following figure gives us an idea about the signs of different trigonometric functions. The angle measured in the counter clockwise direction is taken as positive and angle measured in the clockwise direction is taken as negative.