Question

prove that $x$, and 4, $z$ are in H.P. If $a, a_1, a_2, a_3, ..., a_{2n}, b$ are in A.P. and $a, g_1, g_2, g_3, ..., g_{2n}, b$ are in G.P. and $h$ is the H.M. of $a$ and $b$, then prove that

$\frac{a_1+a_{2n}}{g_1g_{2n}}+\frac{a_2+a_{2n-1}}{g_2g_{2n-1}}+...+\frac{a_n+a_{n+1}}{g_ng_{n+1}}=\frac{2n}{h}$

Answer 1

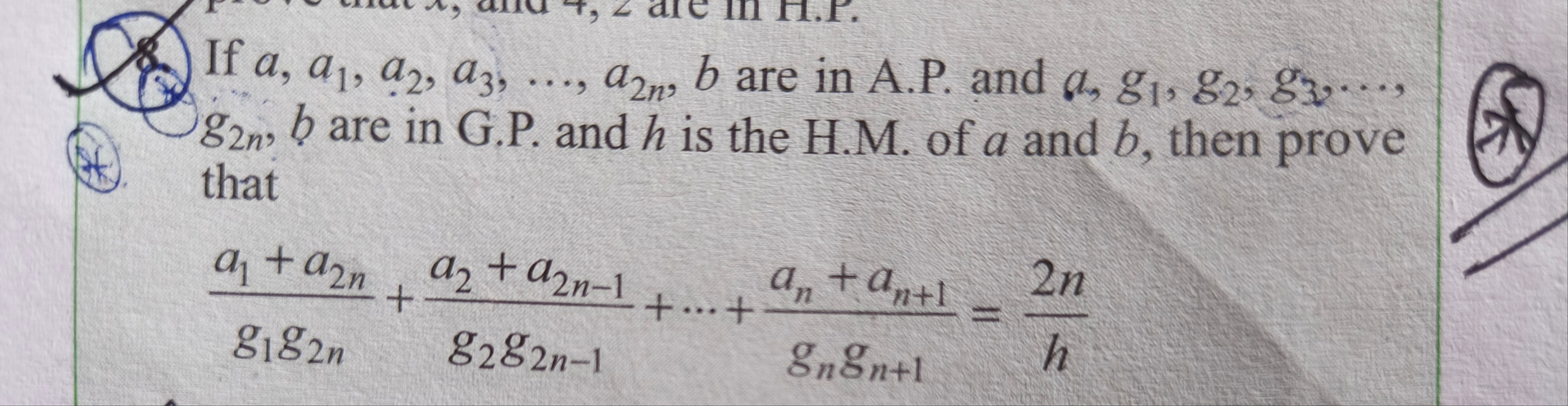
Proof Provided

Answer 2

The question consists of two parts.

Part 1: Condition for $x, 4, z$ to be in H.P.

This statement is grammatically ambiguous and lacks context. To "prove" that $x, 4, z$ are in H.P. would require specific values or conditions for $x$ and $z$, which are not provided. Instead, we can state the condition under which $x, 4, z$ are in H.P.

Condition for $x, 4, z$ to be in H.P.:

By definition, three numbers $A, B, C$ are in H.P. if their reciprocals $\frac{1}{A}, \frac{1}{B}, \frac{1}{C}$ are in A.P. If $x, 4, z$ are in H.P., then $\frac{1}{x}, \frac{1}{4}, \frac{1}{z}$ must be in A.P. For three terms to be in A.P., the middle term is the arithmetic mean of the other two:

$$\frac{1}{4} = \frac{\frac{1}{x} + \frac{1}{z}}{2}$$

Multiplying both sides by 2:

$$\frac{2}{4} = \frac{1}{x} + \frac{1}{z}$$ $$\frac{1}{2} = \frac{1}{x} + \frac{1}{z}$$

This is the condition for $x, 4, z$ to be in H.P. Without any further information or context, one cannot "prove" that arbitrary $x, 4, z$ satisfy this condition.

Part 2: Proof of $\frac{a_1+a_{2n}}{g_1g_{2n}}+\frac{a_2+a_{2n-1}}{g_2g_{2n-1}}+...+\frac{a_n+a_{n+1}}{g_ng_{n+1}}=\frac{2n}{h}$

Given Information:

1. $a, a_1, a_2, ..., a_{2n}, b$ are in A.P.
   This is an A.P. with $2n+2$ terms. Let the common difference be $d$.
   The terms are $a, a+d, a+2d, ..., a+(2n)d, a+(2n+1)d$.
   So, $a_k = a+kd$ for $k=1, 2, ..., 2n$.
   The last term $b = a+(2n+1)d$, which implies $(2n+1)d = b-a$.

2. $a, g_1, g_2, ..., g_{2n}, b$ are in G.P.
   This is a G.P. with $2n+2$ terms. Let the common ratio be $r$.
   The terms are $a, ar, ar^2, ..., ar^{2n}, ar^{2n+1}$.
   So, $g_k = ar^k$ for $k=1, 2, ..., 2n$.
   The last term $b = ar^{2n+1}$, which implies $r^{2n+1} = \frac{b}{a}$.

3. $h$ is the H.M. of $a$ and $b$.
   By definition of Harmonic Mean, $h = \frac{2ab}{a+b}$.

Properties of A.P. and G.P.:

• For A.P.: In an arithmetic progression, the sum of terms equidistant from the beginning and end is constant and equal to the sum of the first and last terms.
  For the A.P. $a, a_1, ..., a_{2n}, b$, the first term is $a$ and the last term is $b$.
  Consider the terms $a_k$ and $a_{2n-k+1}$.
  $a_k = a+kd$
  $a_{2n-k+1} = a+(2n-k+1)d$
  Sum: $a_k + a_{2n-k+1} = (a+kd) + (a+(2n-k+1)d) = 2a + (k+2n-k+1)d = 2a+(2n+1)d$.
  Since $(2n+1)d = b-a$, we have:

  $$a_k + a_{2n-k+1} = 2a + (b-a) = a+b$$

  This holds for all $k=1, 2, ..., n$.

• For G.P.: In a geometric progression, the product of terms equidistant from the beginning and end is constant and equal to the product of the first and last terms.
  For the G.P. $a, g_1, ..., g_{2n}, b$, the first term is $a$ and the last term is $b$.
  Consider the terms $g_k$ and $g_{2n-k+1}$.
  $g_k = ar^k$
  $g_{2n-k+1} = ar^{2n-k+1}$
  Product: $g_k g_{2n-k+1} = (ar^k)(ar^{2n-k+1}) = a^2 r^{k+2n-k+1} = a^2 r^{2n+1}$.
  Since $r^{2n+1} = \frac{b}{a}$, we have:

  $$g_k g_{2n-k+1} = a^2 \left(\frac{b}{a}\right) = ab$$

  This holds for all $k=1, 2, ..., n$.

Evaluating the Left Hand Side (LHS) of the expression to be proven:

The LHS is a sum of $n$ terms:

$$LHS = \frac{a_1+a_{2n}}{g_1g_{2n}}+\frac{a_2+a_{2n-1}}{g_2g_{2n-1}}+...+\frac{a_n+a_{n+1}}{g_ng_{n+1}}$$

Using the properties derived above, for each term in the sum:

• The numerator $a_k+a_{2n-k+1} = a+b$.
• The denominator $g_k g_{2n-k+1} = ab$.

Therefore, each term in the sum is $\frac{a+b}{ab}$.
Since there are $n$ terms in the sum (from $k=1$ to $n$):

$$LHS = \sum_{k=1}^{n} \left(\frac{a+b}{ab}\right) = n \cdot \left(\frac{a+b}{ab}\right)$$

Evaluating the Right Hand Side (RHS) of the expression to be proven:

The RHS is $\frac{2n}{h}$.
From the definition of $h$, we have $h = \frac{2ab}{a+b}$.
This means $\frac{1}{h} = \frac{a+b}{2ab}$.
Substitute this into the RHS:

$$RHS = 2n \cdot \frac{1}{h} = 2n \cdot \left(\frac{a+b}{2ab}\right)$$ $$RHS = n \cdot \left(\frac{a+b}{ab}\right)$$

Conclusion:

Since LHS $= n \cdot \left(\frac{a+b}{ab}\right)$ and RHS $= n \cdot \left(\frac{a+b}{ab}\right)$, we have LHS = RHS.
Hence, the identity is proven.

Solution:

Part 1: Condition for $x, 4, z$ to be in H.P.

If $x, 4, z$ are in H.P., then their reciprocals $\frac{1}{x}, \frac{1}{4}, \frac{1}{z}$ are in A.P.
Thus,

$$\frac{1}{4} = \frac{\frac{1}{x} + \frac{1}{z}}{2}$$ $$\frac{1}{2} = \frac{1}{x} + \frac{1}{z}$$

Part 2: Proof of the identity

Given:

1. $a, a_1, ..., a_{2n}, b$ are in A.P.
   The sum of terms equidistant from the beginning and end is constant:
   $a_k + a_{2n-k+1} = a+b$ for $k=1, ..., n$.
   (This is because $a_k = a+kd_A$ and $a_{2n-k+1} = a+(2n-k+1)d_A$, where $(2n+1)d_A = b-a$. So, $a_k+a_{2n-k+1} = 2a+(2n+1)d_A = 2a+(b-a) = a+b$.)

2. $a, g_1, ..., g_{2n}, b$ are in G.P.
   The product of terms equidistant from the beginning and end is constant:
   $g_k g_{2n-k+1} = ab$ for $k=1, ..., n$.
   (This is because $g_k = ar_G^k$ and $g_{2n-k+1} = ar_G^{2n-k+1}$, where $r_G^{2n+1} = b/a$. So, $g_k g_{2n-k+1} = a^2 r_G^{2n+1} = a^2(b/a) = ab$.)

3. $h$ is the H.M. of $a$ and $b$.
   $h = \frac{2ab}{a+b} \implies \frac{1}{h} = \frac{a+b}{2ab}$.

Consider the Left Hand Side (LHS) of the identity:

$$LHS = \sum_{k=1}^{n} \frac{a_k+a_{2n-k+1}}{g_k g_{2n-k+1}}$$

Substitute the derived properties:

$$LHS = \sum_{k=1}^{n} \frac{a+b}{ab}$$

Since $\frac{a+b}{ab}$ is constant for each term and there are $n$ terms in the sum:

$$LHS = n \cdot \frac{a+b}{ab}$$

Now, consider the Right Hand Side (RHS) of the identity:

$$RHS = \frac{2n}{h}$$

Substitute the expression for $\frac{1}{h}$:

$$RHS = 2n \cdot \left(\frac{a+b}{2ab}\right)$$ $$RHS = n \cdot \frac{a+b}{ab}$$

Since LHS = RHS, the identity is proven.