Question

Prove that the two parabolas, having the same focus and their axes at opposite directions, cut at right angles.

Answer 1

The two parabolas of same focus $\left( a,0 \right)$ having opposite axes are shown in the below figure.

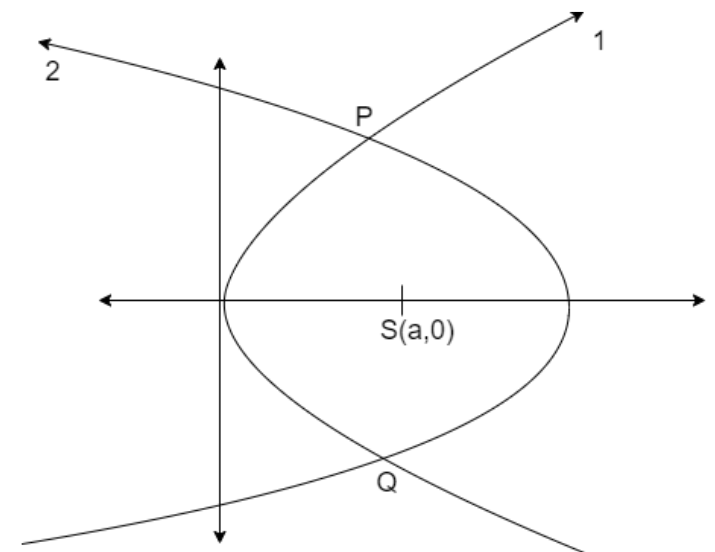
We assume that the equation of the first parabola as ${{y}^{2}}=4ax$ then the equation of parabola having same focus but the opposite axis is given as ${{y}^{2}}=-4a\left( x-2a \right)$ then we find the slopes of tangents of both curves at the intersection point so as to prove the product of tangents at intersection point equal to -1 which proves that the curves cut at right angles.

Complete step-by-step solution:
Let us assume that the equation of the first parabola as
$\Rightarrow {{y}^{2}}=4ax....equation(i)$
Then we know that the equation of parabola having the same focus but opposite direction of the axis is given as
$\Rightarrow {{y}^{2}}=-4a\left( x-2a \right)........equation(ii)$
Now, let us assume that the point of intersection of both the curves as P
Let us find the point P by solving both the equations of parabolas.
By combining both the equations of parabolas we get

& \Rightarrow 4ax=-4a\left( x-2a \right) \\\ & \Rightarrow 2ax=2a \\\ & \Rightarrow x=a \\\ \end{aligned}$$ By substituting the value of $$'x'$$ in equation (i) we get $$\begin{aligned} & \Rightarrow {{y}^{2}}=4a\left( a \right) \\\ & \Rightarrow y=\pm 2a \\\ \end{aligned}$$ Here, we can see that for each value of $$'y'$$ we get two points of intersection. Let us assume that one point as $$P\left( a,2a \right)$$ Now let us find the slopes of tangents of two curves at point $$P\left( a,2a \right)$$ Let us assume that the slope of tangent of equation (i) at $$P\left( a,2a \right)$$ as $${{m}_{1}}$$ given as $$\dfrac{dy}{dx}$$ By taking the equation (i) and differentiating with respect to $$'x'$$ we get $$\Rightarrow \dfrac{d}{dx}\left( {{y}^{2}} \right)=\dfrac{d}{dx}\left( 4ax \right)$$ $$\begin{aligned} & \Rightarrow 2y\dfrac{dy}{dx}=4a \\\ & \Rightarrow {{m}_{1}}=\dfrac{2a}{y} \\\ \end{aligned}$$ Now, by substituting the point $$P\left( a,2a \right)$$ in above equation we get $$\begin{aligned} & \Rightarrow {{m}_{1}}=\dfrac{2a}{2a} \\\ & \Rightarrow {{m}_{1}}=1 \\\ \end{aligned}$$ Let us assume that the slope of tangent of equation (ii) at $$P\left( a,2a \right)$$ as $${{m}_{2}}$$given as $$\dfrac{dy}{dx}$$ By taking the equation (ii) and differentiating with respect to $$'x'$$ we get $$\Rightarrow \dfrac{d}{dx}\left( {{y}^{2}} \right)=\dfrac{d}{dx}\left( -4ax+8{{a}^{2}} \right)$$ $$\begin{aligned} & \Rightarrow 2y\dfrac{dy}{dx}=-4a \\\ & \Rightarrow {{m}_{2}}=-\dfrac{2a}{y} \\\ \end{aligned}$$ Now, by substituting the point $$P\left( a,2a \right)$$ in above equation we get $$\begin{aligned} & \Rightarrow {{m}_{2}}=-\dfrac{2a}{2a} \\\ & \Rightarrow {{m}_{2}}=-1 \\\ \end{aligned}$$ Now, let us find the product of slopes of tangents of both curves we get $$\Rightarrow {{m}_{1}}\times {{m}_{2}}=-1$$ Here, we can see that the product of slopes of tangents at the point of intersection is -1 Therefore we can conclude that the curves cut at right angles. Hence the required result has been proved. **Note:** We can solve the above result using the other point also that is $$Q\left( a,-2a \right)$$ Now let us find the slopes of tangents of two curves at point $$Q\left( a,-2a \right)$$ Let us assume that the slope of tangent of equation (i) at $$Q\left( a,-2a \right)$$ as $${{m}_{1}}$$ given as $$\dfrac{dy}{dx}$$ By taking the equation (i) and differentiating with respect to $$'x'$$ we get $$\Rightarrow \dfrac{d}{dx}\left( {{y}^{2}} \right)=\dfrac{d}{dx}\left( 4ax \right)$$ $$\begin{aligned} & \Rightarrow 2y\dfrac{dy}{dx}=4a \\\ & \Rightarrow {{m}_{1}}=\dfrac{2a}{y} \\\ \end{aligned}$$ Now, by substituting the point $$Q\left( a,-2a \right)$$ in above equation we get $$\begin{aligned} & \Rightarrow {{m}_{1}}=\dfrac{2a}{\left( -2a \right)} \\\ & \Rightarrow {{m}_{1}}=-1 \\\ \end{aligned}$$ Let us assume that the slope of tangent of equation (ii) at $$Q\left( a,-2a \right)$$ as $${{m}_{2}}$$ given as $$\dfrac{dy}{dx}$$ By taking the equation (ii) and differentiating with respect to $$'x'$$ we get $$\Rightarrow \dfrac{d}{dx}\left( {{y}^{2}} \right)=\dfrac{d}{dx}\left( -4ax+8{{a}^{2}} \right)$$ $$\begin{aligned} & \Rightarrow 2y\dfrac{dy}{dx}=-4a \\\ & \Rightarrow {{m}_{2}}=-\dfrac{2a}{y} \\\ \end{aligned}$$ Now, by substituting the point $$Q\left( a,-2a \right)$$ in above equation we get $$\begin{aligned} & \Rightarrow {{m}_{2}}=-\dfrac{2a}{\left( -2a \right)} \\\ & \Rightarrow {{m}_{2}}=1 \\\ \end{aligned}$$ Now, let us find the product of slopes of tangents of both curves we get $$\Rightarrow {{m}_{1}}\times {{m}_{2}}=-1$$ Here, we can see that the product of slopes of tangents at the point of intersection is -1 Therefore we can conclude that the curves cut at right angles. Hence the required result has been proved.