Solveeit Logo
Login

Question

Question: Prove that the trigonometric expression \(2{\tan ^{ - 1}}x = {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 +...

Prove that the trigonometric expression 2tan⁡−1x=sin⁡−1(2x1+x2)2{\tan ^{ - 1}}x = {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right) holds true.

Explanation

Solution

Hint – In this question consider the L.H.S part and break 2tan⁡−1x2{\tan ^{ - 1}}x into tan⁡−1x+tan⁡−1x{\tan ^{ - 1}}x + {\tan ^{ - 1}}x, then apply the formulatan⁡−1A+tan⁡−1B=tan⁡−1(A+B1−AB){\tan ^{ - 1}}A + {\tan ^{ - 1}}B = {\tan ^{ - 1}}\left( {\dfrac{{A + B}}{{1 - AB}}} \right). Then convert trigonometric identity of tan⁡−1x into sin−1x{\tan ^{ - 1}}x{\text{ into si}}{{\text{n}}^{ - 1}}x to get the proof.

Complete step-by-step solution -


Proof –
Consider L.H.S
⇒2tan⁡−1x\Rightarrow 2{\tan ^{ - 1}}x
This is written as
⇒tan⁡−1x+tan⁡−1x\Rightarrow {\tan ^{ - 1}}x + {\tan ^{ - 1}}x
Now as we know that tan⁡−1A+tan⁡−1B=tan⁡−1(A+B1−AB){\tan ^{ - 1}}A + {\tan ^{ - 1}}B = {\tan ^{ - 1}}\left( {\dfrac{{A + B}}{{1 - AB}}} \right) so use this property in above equation we have,
⇒tan⁡−1x+tan⁡−1x=tan⁡−1(x+x1−x2)=tan⁡−1(2x1−x2)\Rightarrow {\tan ^{ - 1}}x + {\tan ^{ - 1}}x = {\tan ^{ - 1}}\left( {\dfrac{{x + x}}{{1 - {x^2}}}} \right) = {\tan ^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)
Now let
y = tan⁡−1(2x1−x2){\tan ^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)................. (1)
⇒tan⁡y=(2x1−x2)\Rightarrow \tan y = \left( {\dfrac{{2x}}{{1 - {x^2}}}} \right)
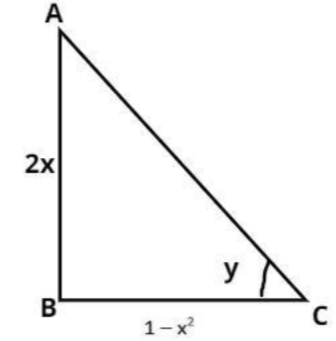
Now as we know tan is ratio of perpendicular to base
Therefore perpendicular = 2x
And base = (1–x2)(1 – {x^2}).
Now apply Pythagoras theorem in right triangle ABC as shown above we have,
⇒(Hypotenuse)2=(perpendicular)2+(base)2\Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}
⇒(Hypotenuse)2=(2x)2+(1−x2)2\Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {2x} \right)^2} + {\left( {1 - {x^2}} \right)^2}
Now simplify this we have,
⇒(Hypotenuse)2=4x2+1+x4−2x2=1+2x2+x4=(1+x2)2\Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = 4{x^2} + 1 + {x^4} - 2{x^2} = 1 + 2{x^2} + {x^4} = {\left( {1 + {x^2}} \right)^2}
Therefore, (Hypotenuse)=(1+x2)\left( {{\text{Hypotenuse}}} \right) = \left( {1 + {x^2}} \right)
Now as we know sin is the ratio of perpendicular to hypotenuse so we have,
⇒sin⁡y=2x1+x2\Rightarrow \sin y = \dfrac{{2x}}{{1 + {x^2}}}
⇒y=sin⁡−1(2x1+x2)\Rightarrow y = {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right)
So from equation (1) we have,
⇒tan⁡−1(2x1−x2)=sin⁡−1(2x1+x2)\Rightarrow {\tan ^{ - 1}}\left( {\dfrac{{2x}}{{1 - {x^2}}}} \right) = {\sin ^{ - 1}}\left( {\dfrac{{2x}}{{1 + {x^2}}}} \right)
= L.H.S
Hence proved.

Note – The conversion of one inverse trigonometric identity into another is based upon the same concept as that of conversion of a normal trigonometric ratio into another. A right angled triangle depicting sides of perpendicular, base and hypotenuse, helps establish relations.