Question

Prove that the time of flight 'T' and horizontal range 'R' of a projectile motion are connected by the equation $g{T^2} = 2Rtan\theta$.

Answer 1

Consider the projectile motion to be the sum of two rectilinear motion in x-axis and y-axis.
Apply equations of motion separately in these two motions:
$\begin{gathered} v = u + at \\\ s = ut + \dfrac{1}{2}a{t^2} \\\ {v^2} = {u^2} + 2as \\\ \end{gathered}$
Where, u = initial velocity, v = final velocity, s = displacement, a = acceleration and t = time.
Time of flight is the total time taken to complete the projectile motion, it will be double the time taken to reach the maximum height. Hence, calculate time to reach maximum height by using equation $v = u + at$ and taking v = 0 for maximum height.
And the horizontal range is the displacement of the projectile in x direction. Since, there is no acceleration in x direction so it can be simply calculated using equation $s = ut$, where we have to put u the horizontal velocity and t the time of flight.

Complete step by step answer:
Let us consider a ball projected at an angle θ with respect to the horizontal x-axis with the initial velocity u as shown below:

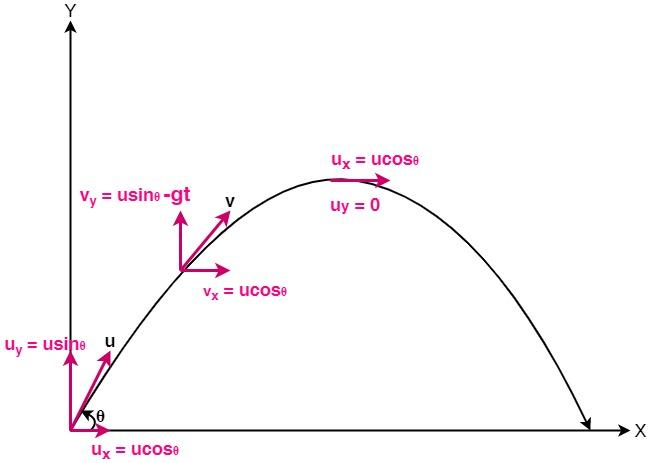
In a Projectile Motion, there are always two simultaneous independent rectilinear motions happening:
1. Along the x-axis: along x-axis velocity is uniform which is responsible for the horizontal (forward) motion of the particle.
2. Along y-axis: The particle is moving with a uniform acceleration but varying velocity which is responsible for the vertical (downwards) motion of the particle.
The x components and y components of the initial velocity can be expressed as:

{u_x} = u \cdot cos\theta \\\ {u_y} = u \cdot sin\theta \\\ \end{gathered} $$ Accelerations in the horizontal and vertical motions of the particle moving in projectile can be expressed as: There is no acceleration in the horizontal motion of the particle moving in projectile. $$ \Rightarrow {a_x} = 0$$ The acceleration in the vertical motion of the particle in projectile is just due to acceleration due to gravity: $${a_y} = - g\,\left( {downward} \right)$$ The velocity of the particle moving in projectile at any point in path of projectile can be given as: The horizontal velocity remains constant, $$ \Rightarrow {v_x} = u \cdot cos\theta $$ But the vertical velocity varies linearly, because the acceleration is constant. At any time, t, the velocity is: $${v_y} = u \cdot sin\theta - g \cdot t{\text{ }}\left( {{\text{from eq}}{\text{. of motion: v = u + at}}} \right)$$ Now, finding: 1\. Time of flight: As we know velocity at max height, v = 0 Using: $$\begin{array}{*{20}{l}} {V{\text{ }} = {\text{ u }} + {\text{ }}at} \\\ { \Rightarrow 0{\text{ }} = {\text{ us}}in\theta {\text{ }} - {\text{ }}gt} \\\ { \Rightarrow {\text{ t }} = {\text{ }}\dfrac{{\;using\theta }}{g}} \end{array}$$ Ball will take the same time to return to the ground. Time of flight : $$\begin{gathered} = 2 \times t \\\ \; = {\text{ }}2\dfrac{{using\theta }}{g} \\\ \begin{array}{*{20}{l}} { \Rightarrow T{\text{ }} = {\text{ }}2\dfrac{{u\sin \theta }}{g}{\text{ - - - - - - - - - - - - [1]}}} \\\ {} \end{array} \\\ \end{gathered} $$ Horizontal Range = Horizontal Velocity x Flight Time Hence, proved. **Note:** In projectile motion at any time t, the displacement components are given by: $$\begin{gathered} x = ucos\theta \cdot t \\\ y = usin\theta \cdot t - \dfrac{1}{2}g{t^2}{\text{ }}\left( {{\text{from eq}}{\text{. of motion: s = ut + }}\dfrac{1}{2}a{t^2}} \right) \\\ \end{gathered} $$ These equations can be used to solve various problems, you just have to apply equations of motion in projectile motion by considering its independent rectilinear motion along x-axis and y-axis.