Question

Prove that the tangents drawn at the endpoints of a chord of a circle make equal angles with the chord.

Answer 1

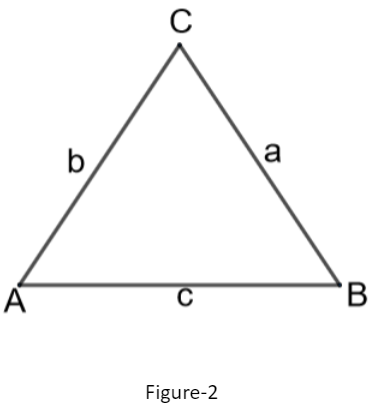
To solve this question, we should use the properties related to tangent and the circle. We know a property that the tangent at a point on the circle is perpendicular to the line joining the point and the center of the circle. Using this property and the congruence of the triangles, we can prove that the length of the tangents from an external point to the circle are equal. Now, we should use the property related to the triangles which are known as the sine rule. In a triangle with the length of the sides as $a,b,c$ and the corresponding opposite angles be $A, B, C$ as shown in figure-2, the sine rule states that
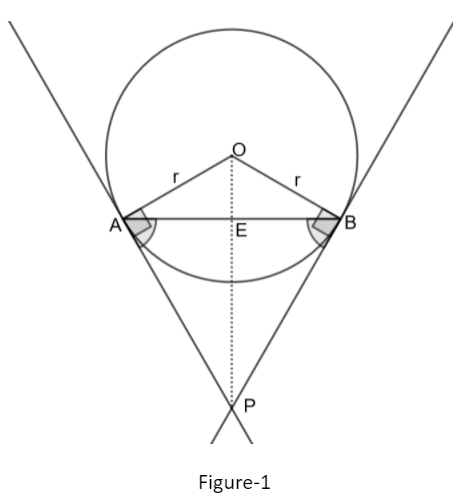
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$. Using this rule in the triangle ABP in the below figure-1, we get the required result.

Complete step-by-step solution:
__
__

In the above figure, O is the center of the circle with radius r units, AP and BP are the tangents to the circle at the endpoints of the chord AB. OA and OB are line segments, which are equal to the radius of the circle. We should prove that $\angle ABP=\angle BAP$.
Let us consider the triangles $\Delta OAP,\Delta OBP$.
From the property that the tangent at a point of the circle is perpendicular to the line joining the point and the centre of the circle, we can write that
$\begin{aligned} & \angle OAP={{90}^{\circ }} \\\ & \angle OBP={{90}^{\circ }} \\\ & \angle OAP=\angle OAP={{90}^{\circ }} \\\ \end{aligned}$
As the line segments OA and OB are both equal to radius, we can write that
$OA=OB=r$
OP is the common side of the two triangles.
From the SAS(Side, Angle, Side) property of the triangles, which states that two triangles are congruent if two corresponding sides and a corresponding angle are equal in both the triangles, we can write that
$\Delta OAP\approx \Delta OBP$
The corresponding sides of the congruent triangles are equal. Using this, we can write that $AP=BP$.
This is also called the length of the tangent property which states that the length of the two tangents from an external point are equal.
Now, let us consider the triangle $\Delta APB$
We can infer that it is an isosceles triangle with equal sides as $AP=BP$.
We should use the property related to the triangles which is known as the sine rule. In a triangle with the length of the sides as $a,b,c$ and the corresponding opposite angles be $A, B, C$ as shown in figure-2, the sine rule states that
$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$.

Using this property, we can write that
$\dfrac{AP}{\sin \left( \angle ABP \right)}=\dfrac{BP}{\sin \left( \angle BAP \right)}$
Using the result $AP=BP$ and canceling the terms, we get
$\sin \left( \angle ABP \right)=\sin \left( \angle BAP \right)$
As both the angles are angles of a triangle, their sum must be less than ${{180}^{\circ }}$ and the above equality is only possible when both the angles are equal.
$\angle ABP=\angle BAP$
$\therefore$ Proved that the tangents drawn at the endpoints of a chord of a circle make equal angles with the chord.

Note: An alternative way to prove the statement is by using the property that the line joining the center of the circle and the point of intersection of the tangents acts as an angular bisector for the included angle of the tangents. In our question, we can write this as OP is an angular bisector of the angle $\angle APB$. Now by considering the triangles $\Delta AEP,\Delta BEP$, we can write that the two triangles are congruent as two sides ($AP=BP$, EP-common side) and angle ($\angle APE=\angle BPE$ )are equal. Hence, we can prove the required result.